|
抓住关键 突破难点 ──平抛运动的处理方法 江苏省靖江市季市中学 范晓波 平抛运动是一种典型的匀变速曲线运动。本身不能够直接运用匀变速直线运动的规律讨论，基本的处理思想是“化曲为直”，即利用运动的分解将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动，再借助直线运动的规律进行处理。 平抛运动分解后，两个方向的分运动性质明确，初速度、加速度也均为已知量，因此，无论最终要求解什么量，找出运动的时间是关键。下面结合实际问题说明一下求解时间的常用方法。 一、利用竖直分速度寻找时间 例：一个小球以初速度 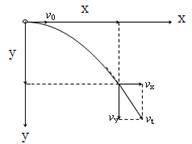 水平抛出，落地速度为 ，空气阻力不计，求小球的起抛高度和水平位移。 分析：平抛运动竖直方向的分速度  与运动的时间有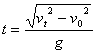关，因此，可以考虑借助 求解运动的时间。解：如图可得  而 则  所以 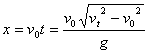 ， 说明：运动时间对平抛运动解决过程的重要性在本题中一目了然，只要找到平抛物体运动的时间，一切问题都能解决。 二、利用竖直位移寻找时间 例：已知排球场内网高 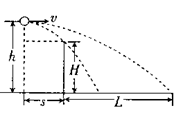 ，半场长 ，扣球点高 ，扣球点离网的水平距离为 ，求：水平扣球速度 的取值范围。 分析：本题中隐含了临界问题，排球作平抛运动的临界轨迹如图，水平位移决定于水平初速度和运动的时间，现在水平位移大小已知，要求水平扣球速度，应先找出排球在空中飞行的时间。 解：排球擦网而过时，设对应的水平初速度为  由  得： 则  排球恰好不出界时，设对应的初速度为  由  得： 则  所以水平扣球速度应满足  说明：平抛物体的运动时间决定于下落高度（即竖直位移大小），因此实际问题常常利用平抛运动的下落高度寻找物体运动的时间。 三、利用末速度方向寻找时间 例：如图，以 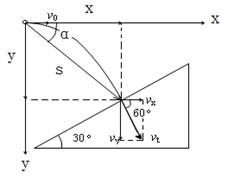 的水平初速度抛出的物体，飞行一段时间后，垂直地撞在倾角为 的斜面上，物体完成这段飞行的总位移是多少？ 分析：物理学中，矢量的方向一般用角度定量描述。既然物体的末速度方向与斜面垂直，而斜面倾角是个已知量，那么末速度的方向也就已经明确。 解：如图，物体的末速度与水平方向的夹角为  又  则  所以    且  ，即与水平方向成 角斜向右下方。说明：该类型问题也可借助 先求出，再转化为第二类问题解决，但求解过程不如上述方法简单，尤其在未知的情况下更是如此。另外，“反向延长交入射线于中点”是一个非常有用的结论，在一些复杂问题中加以使用会有很好的效果。四、利用位移方向寻找时间 例：如图，AB为斜面，倾角为 ，小球从A点以初速度水平抛出，恰好落到B点。求（l）AB间的距离；（2）物体在空中飞行的时间。 说明：小球运动的起点A．终点B均在斜面上，总位移就沿斜面方向，而斜面倾角已知，位移方向也成了已知量。 解：如图，小球的总位移与水平方向夹角为 又 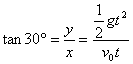 则  所以   说明：借助已知角的正切求运动时间是寻找时间的一种有效方法，但使用时一定要看清已知角是速度矢量三角形的内角还是位移矢量三角形的内角，即表达式右侧到底是两个分速度之比，还是两个分位移之比。 综上所述，平抛运动的解题策略可以用一句话概括，那就是“在分解的前提下，利用 、 的大小或、的方向求解运动的时间”。不仅平抛运动可以如此处理，一切类平抛运动都可以这样处理。五、变式练习 1．飞机距地面高  ，水平飞行速度为 ，追击一辆速度为 同向行驶的汽车，欲使投弹击中汽车，飞机应在距汽车多远处投弹？2．如图所示，光滑斜面长为  ，宽为 ，倾角为 ，一物块沿斜面左上方顶点P水平射入，而从右下方顶点Q离开斜面，求入射的初速度。 3．作平抛运动的物体，在落地前的最后  内，其速度方向由跟竖直方向成角变为跟竖直方向成 角，求：物体抛出时的速度和高度分别是多少？4．如图所示，一个小球从楼梯顶部以  的水平速度抛出，所有的台阶都是高 ，宽 ，问小球从楼梯顶部抛出后首先撞到哪一级台阶上？ 5．如图所示，一高度  的水平面在A点处与一倾角 的斜面连接，一小球以 的速度在水平面上向右运动。求小球从A点运动到地面所需的时间（平面与斜面均光滑，取 ）。某同学对此题的解法为：小球沿斜面运动，则 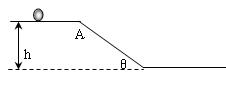 由此可求得落地的时间t。问：你同意上述解法吗？若同意，求出所需的时间；若不同意，则说明理由并求出你认为正确的结果。 变式练习答案： 1．答案：  2．答案：  3．答案：  ； 4．答案：第3级 5．答案：不同意； 
(责任编辑：admin) |