|
天体运动问题习题归类例析 江西省全南中学 李红伟 天体运动问题的本质是牛顿运动定律与万有引力定律的应用问题。本文对中学物理中的天体运动问题进行了归纳总结，希望能帮助师生更好地掌握和解决这类问题。 一、明确一组相互关系 明确一种关系，即明确重力与万有引力的关系。地球不停地自转，地球表面的物体随地球自转需要向心力。此向心力并不是地球对物体的万有引力，而是地球的万有引力与地球表面对物体的支持力的合力。 例：（2010北京卷）一物体静置在平均密度为ρ的球形天体表面的赤道上。已知万有引力常量G，若由于天体自转使物体对天体表面压力恰好为零，则天体自转周期为 Ａ．  Ｂ． Ｃ． Ｄ． 【解析】赤道上表面的物体对天体表面的压力为零，说明天体对物体的万有引力恰好等于物体随天体转动所需要的向心力，由 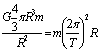 ，化简得 。所以正确答案为D。二、抓住两条解题思路 思路一：在不考虑天体自转的情况下，天体表面的物体可以认为其重力等于天体对它的万有引力，mg =F引。由  得：GM=gR2 ，此式称为“黄金代换公式”。思路二：卫星（行星）绕中心天体的运动可以近似看成匀速圆周运动，中心天体对卫星（行星）的万有引力提供其做匀速圆周运动的向心力，即有：  。三、掌握三类典型问题 1．双星问题 宇宙中往往会有相距较近的两颗星球，它们离其它星球都较远，其它星球对它们的万有引力可以忽略不计；在这种情况下，它们将各自围绕它们连线上的某一固定点做相同周期的匀速圆周运动，这种结构叫做双星。双星具有以下特点：（1）两星都绕它们连线上的一点做匀速圆周运动，两星的角速度相同、周期相等；（2）两星之间的万有引力提供各自做圆周运动的向心力，所以它们的向心力大小相等；（3）两星的轨道半径与其质量成反比，且两半径之和等于两星间距。 另外还有三星，四星等多星天体的运动问题。这类问题中运动天体的向心力是由其他天体的万有引力的合力提供；运动天体的角速度相同、周期相等；但注意天体运动的轨道半径不是天体问题的距离，要利用几何知识，寻找两者之间的关系。 例：（2012重庆卷）冥王星与其附近的星体卡戎可视为双星系统，质量比约为7：1，同时绕它们连线上某点O做匀速圆周运动。由此可知，冥王星绕O点运动的 A．轨道半径约为卡戎的1/7 B．角速度大小约为卡戎的1/7 C．线度大小约为卡戎的7倍 D．向心力大小约为卡戎的7倍 【解析】根据双星轨道半径与其质量成反比，可知冥王星绕O点运动的轨道半径约为卡戎的1/7，故A对；双星的角速度相同，故B错；V=ωR，a=ωv，故C、D错。 2．变轨问题 卫星由于某种原因速度突然改变时（开启或关闭发动机或空气阻力作用），万有引力就不再等于向心力，卫星将变轨运行。 当速度增大时，所需向心力增大，即万有引力不足以提供向心力，卫星将做离心运动，脱离原来的圆轨道，轨道半径变大；但卫星一旦进入新的轨道运行时，由  知，其运行速度要减小（比原轨道速度小），但引力势能、机械能均增加。反之，当速度减小时，所需向心力减小，卫星将做向心运动，轨道半径变小；卫星进入新轨道运行时，运行速度将增大，引力势能、机械能均减小。 例：（2011全国卷Ⅰ）我国“嫦娥一号”探月卫星发射后，先在“24小时轨道”上绕地球运行(即绕地球一圈需要24小时)；然后，经过两次变轨依次到达“48小时轨道”和“72小时轨道”；最后奔向月球。如果按圆形轨道计算，并忽略卫星质量的变化，则在每次变轨完成后与变轨前相比 A．卫星动能增大，引力势能减小 B．卫星动能增大，引力势能增大 C．卫星动能减小，引力势能减小 D．卫星动能减小，引力势能增大 【解析】周期变长，表明轨道半径变大，速度减小，动能减小,引力做负功故引力势能增大，故选D 例：（2012广东卷）如图所示，飞船从轨道1变轨至轨道2，若飞船在两轨道上都做匀速圆周运动，不考虑质量变化，相对于在轨道1上，飞船在轨道2上的 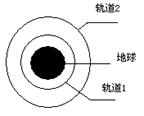 A．动能大 B．向心加速度大 C．运行周期长 D．角速度小 【解析】飞船从轨道1变轨至轨道2，轨道半径变大，速度减小，动能变小，运行周期变长，向心加速度变小，角速度变小，故选C、D。 3．地球同步卫星问题 地球同步卫星是指相对地面静止的、运行周期与地球的自转周期相等的卫星，这种卫星一般用于通讯，又叫做同步通信卫星。地球同步卫星特点可概括为“五个一定”，即：位置一定：必须位于地球赤道的上空；周期一定：  ；高度一定： ；速率一定： ；运行方向一定：自西向东运行。例：（2011全国卷）卫星电话信号需要通地球同步卫星传送。如果你与同学在地面上用卫星电话通话，则从你发出信号至对方接收到信号所需最短时间最接近于（可能用到的数据：月球绕地球运动的轨道半径约为3.8×105m/s，运行周期约为27天，地球半径约为6400千米，无线电信号传播速度为3x108m/s） A．0.1s B．0.25s C．0.5s D．1s 【解析】月球、地球同步卫星绕地球做匀速圆周运动，根据开普勒第三定律  可得同步卫星离地面高度h=35822m ；由T=2h/c=0.24s，故选B。四、区分四对基本概念 1．轨道半径和天体半径 轨道半径是天体的卫星绕天体做圆周运动的圆半径，天体半径是指天体的几何尺寸；对天体的“近地”卫星（或卫星飞行离天体便面高度远小于天体半径），其轨道半径近似等于天体半径。 例：（2012福建卷）一卫星绕某一行星表面附近做匀速圆周运动，其线速度大小为v，假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体重力，物体静止时，弹簧测力计的示数为N，已知引力常量为G,则这颗行星的质量为 A．  B. C． D． 【解析】设该行星半径为R，则行星表面附近的卫星满足  ，物体在行星表面平衡静止时有N= ，由上两式可得M= ，故选B 。2．运行速度和发射速度 发射速度是指卫星在地面附近离开发射装置时的初速度，要发射一颗人造地球卫星，发射速度不能小于第一宇宙速度，即最小发射速度是7.9km/s；若要发射一颗轨道半径大于地球半径的人造卫星，发射速度必须大于7.9km/s。可见，向高轨道发射卫星比向低轨道发射卫星要困难。 运行速度是指卫星在进入运行轨道后绕地球运行时的线速度。当卫星“贴着”地面（即近地）飞行时，运行速度等于第一宇宙速度，当卫星的轨道半径大于地球半径时，运行速度小于第一宇宙速度，所以最大运行速度是7.9km/s。 例：一颗人造地球卫星以初速度v发射后，可绕地球做匀速圆周运动，若使发射速度增为2v，则该卫星可能 A．绕地球做匀速圆周运动 B．绕地球运动，轨道变为椭圆 C．不绕地球运动，成为太阳系的人造卫星 D．挣脱太阳引力的束缚，飞到太阳系以外的宇宙去了 【解析】以初速度v发射后能成为人造地球卫星，可知发射速度v一定大于第一宇宙速度7.9km/s；当以2v速度发射时，发射速度一定大于15.8km/s，已超过了第二宇宙速度11.2km/s，所以此卫星不再绕地球运行，可能绕太阳运行，或者飞到太阳系以外的空间去了，故选项C、D正确。 3.转动向心加速度和自转向心加速度 行星（卫星）绕中心天体转动的向心加速度是由万有引力提供，方向指向天体中心，即a1 = F万/m = GM/r2 ；物体随天体自转的向心加速度是由万有引力的一个分力提供，方向垂直指向自转转轴，即a2= ω自2·R＝(  )2·R 。例：同步卫星的加速度为a1，地面附近卫星的加速度为a2，地球赤道上物体随地球自转的向心加速度为a3，则 A．a1>a2>a3 B．a3>a2>a1 C．a2>a3>a1 D．a2>a1>a3 【解析】因为同步卫星和地球赤道上物体的角速度相同，又因为a=ω2r，r1>r3；所以a1>a3 ；地面附近卫星的加速度为a2=g,为最大，所以a2>a1>a3 。所以正确答案是D 。 4．自转周期和公转周期 自转周期是天体绕自身某轴线转动一周的时间，公转周期是卫星绕中心天体做圆周运动一周的时间。一般情况下天体的自转周期和公转周期是不等的，如地球自转周期为24小时，公转周期为365天。但也有相等的，如月球自转公转周期都约为27天，也是这个原因，地球上永远只能看到月球的一面。 例：（10全国卷Ⅱ）已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半，它的同步卫星距其表面的高度是其半径的2.5倍，则该行星的自转周期约为 A．6小时 B. 12小时 C. 24小时 D. 36小时 【解析】地球的同步卫星的周期为T1=24小时，轨道半径为r1=7R1，密度ρ1。某行星的同步卫星周期为T2，轨道半径为r2=3.5R2，密度ρ2。根据牛顿第二定律和万有引力定律分别有 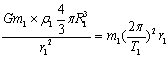 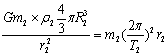 两式化简得T2=T1/2=12小时，所以正确答案是B 。 (责任编辑：admin) |