|
机械能问题的常见题型 陕西省宝鸡市陈仓区教育局教研室 邢彦君 机械能是物理学的重要概念，涉及机械能的问题是高考试题中的必考问题。这类试题有力学综合问题，也有力电综合问题；有机械能守恒问题，也有机械能不守恒问题。机械能守恒问题可运用机械能守恒定律分析求解，机械能不守恒问题，一般运用动能定理或能量守恒定律分析求解。 1．机械能守恒条件问题 机械能包括动能、重力势能、弹性势能，其中的重力势能是物体与地球共有的。因此，机械能守恒针对的是物体、弹簧（或发生弹性形变的其它物体）和地球组成的系统，而不是某个单独的物体。若这个系统在运动过程中，内部各物体间相互作用的力中，只有重力、弹力做功，这一运动过程中系统的机械能总量保持不变。这就是机械能守恒的条件，欲运用机械能守恒定律分析求解物理问题，应首先选择有相互作用的物体系统，然后分析在运动过程中系统内各物体间的相互作用力。若系统内只有重力、弹力，或虽有非重力、弹力作用但这些力不做功或所做功的代数和等于零，则系统的运动过程中，机械能总量保持不变。 例1．一蹦极运动员身系弹性蹦极绳从水面上方的高台下落，到最低点时距水面还有数米距离。假定空气阻力可忽略，运动员可视为质点，下列说法正确的是 A．运动员到达最低点前重力势能始终减小 B．蹦极绳张紧后的下落过程中，弹性力做负功，弹性势能增加 C．蹦极过程中，运动员、地球和蹦极绳所组成的系统机械能守恒 D．蹦极过程中，重力势能的改变与重力势能零点的选取有关 解析：运动员到达最低位置前，一直向下运动，重力一直做正功，重力势能一直是减小的。A对；蹦极绳张紧后，随着运动员的继续下降，绳伸长，对运动员作用向上的弹性力，此力做负功，绳的弹性势能增加。B对；由于空气阻力可以忽略，蹦极过程中，对于运动员、地球、绳系统来说，只有重力与弹性绳的弹性力做功，系统的机械能守恒。C对；重力势能与重力势能参考平面的选取有关，而重力势能的变化量则与此无关。D错。本题选ABC。 【点评】做功不做功，决定与此功对应的能量是否变化，功的正负决定能的增减。重力做正功（或负功）重力势能减少（或增加）；弹簧的弹力做正功（或负功）弹簧的弹性势能减少（或增加）。 2．机械能守恒过程中的动态问题 机械能守恒时物体系统机械能总量保持不变。这一过程中，由于系统内部的重力、弹力做功，会发生重力势能、动能和弹性势能在系统内部各物体间的转化或转移，并非各种形式的机械能都保持不变。因此，机械能的守恒，是一种动态的守恒，守恒中有能转化或转移，重力做功对应重力势能的变化，弹力做功对应弹性是能的变化，合力做功对应功能的变化。 例2．如图1（甲）所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复。通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图像如图（乙）所示，则 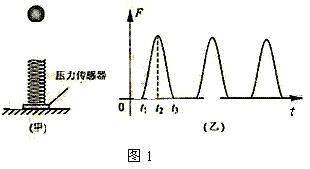 A．t1时刻小球动能最大 B．t2时刻小球动能最大 C．t2-t3这段时间内，小球的动能先增加后减少 D．t2-t3这段时间内，小球增加的动能等于弹簧减少的弹性势能 解析：由图象可知，t1时刻，小球刚接触弹簧，此后，至小球经过平衡位置，弹簧对小球向上的弹力小于向下的重力，这两个力的合力向下，对小球做正功，小球的动能增加。小球过了平衡位置后，向上的弹力大于向下的重力，两者合力方向向上，对小球做负功，小球动能开始减小，因此，小球过平衡位置时的动能最大。而图象中的t2时刻，小球已落至最低点，动能为零。A、B错；t2-t3这段时间内，小球由最低点向上运动到弹簧恢复原长，先是向上的弹力大于向下的重力，两者的合力向上，对小球做正功，小球动能增加，过平衡位置后，弹簧弹力小于重力，两者合力方向向下，对小球做负功，小球动能减少。由于只有重力及弹簧的弹力做功，因此，小球、地球、弹簧系统的机械能守恒，这一过程中弹簧减少的弹性势能转化成了小球的动能与重力势能，小球增加的动能等于弹簧减少的弹性势能与小球增加的重力势能的差。C对D错。本题选C。 【点评】对于物体落在竖直弹簧上的运动，平衡位置（加速度为零）是物体速度增加与减小的临界位置。 3．机械能守恒的力学综合问题 如果运动中物体系统的机械能守恒，对系统的运动过程可运用机械能守恒定律列出方程，依据解题的需要对其中的某物体的某个状态，运用牛顿第二定律在列方程，然后连理求解。 例3．如图2所示，长度为l的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小可以忽略）。 （1）在水平拉力F的作用下，轻绳与竖直方向的夹角为α，小球保持静止，画出此时小球的受力图，并求力F的大小。 （2）由图示位置无初速度释放小球，求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。 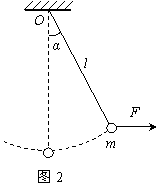  解析：（1）小球受力示意图如图3所示。由共点力平衡条件有：  ， ，解得力F的大小为： 。（2）运动中，小球、轻绳、地球系统中，只有重力做功，机械能守恒。对小球从释放到经过最低点的运动由动能定理有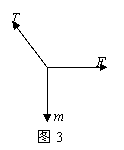：  ，解得小球通过最低点时的速度大小为： 。对小球通过最低点时的运动运用牛顿第二定律有：  。解得轻绳对小球的拉力为： ，方向竖直向上。  【点评】机械能守恒定律适用于机械能守恒的运动过程，牛顿第二定律则适用于运动过程中的状态。 4．机械能不守恒的力学综合问题 若运动中，系统内部的力中有非重力、弹力做功且这些功的代数和不等于零，运动过程中系统的机械能肯定不守恒。这类问题，可运用动能定理或能量守恒定律分析求解。 例4．某兴趣小组设计了如图4所示的玩具轨道，其中“2008”四个等高数字用内壁光滑的薄壁细圆管弯成，固定在竖直平面内（所有数字均由圆或半圆组成，圆半径比细管的内径大得多），底端与水平地面相切。弹射装置将一个小物体（可视为质点）以va=5m/s的水平初速度由a点弹出，从b点进入轨道，依次经过“8002”后从p点水平抛出。小物体与地面ab段间的动摩擦因数μ=0.3，不计其它机械能损失。已知ab段长L=l.5m，数字“0”的半径R=0.2m，小物体质量m=0.0lkg，g=10m/s2。求：   （1）小物体从p点抛出后的水平射程； （2）小物体经过数字“0”的最高点时管道对小物体作用力的大小和方向。 解析：（1）设小物体运动到p点（或过“0”的最高点）时的速度大小为v，对小物体由a运动到p过程应用动能定理得：  ，小物体自p点做平抛运动，设运动时间为t．水平射程为s，则有： 和 。代入数据解以上几式得：s=0.8m ， 。（2）设在数字“0”的最高点时管道对小物体的作用力大小为F，取竖直向下为正方向，由牛顿第二定律有：  ，代入数据解得：F=0.3N ，方向竖直向下。【点评】小球在ab段的运动机械能不守恒，在bp段的运动机械能守恒，但整个运动阶段机械能不守恒。将整个阶段视为整体运用动能定理简化了解题过程。 5．涉及电场的力电综合问题 带电粒子在电场中运动，由于电场力做功，物体系统的机械能不守恒。这类问题，一般运用动能定律、能量守恒定律及电场等知识分析求解。 例5．如图5所示，在水平地面上固定一倾角为θ的光滑绝缘斜面，斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中。劲度系数为k的绝缘轻弹簧一端固定在斜面底端，处于自然状态。质量为m、带电量为q（q>0）的滑块从距弹簧上端so处由静止释放，滑块运动过程中电量保持不变。设滑块与弹簧接触过程没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g。  （1）求滑块从释放到与弹簧上端接触瞬间所经历的时间；（2）若滑块在沿斜面向下运动的整个过程中最大速度大小为vm，求滑块从释放到速度大小为vm过程中弹簧的弹力所做的功W。 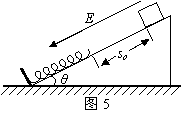  解析： （1）带电滑块从静止释放到与弹簧刚接触的过程中，做初速度为零的匀加速直线运动，设加速度大小为a，由牛顿第二定律及匀变速直线运动位移公式有： ， 。解得： 。（2）带电滑块与弹簧接触后的运动中，在斜面方向受重力沿斜面向下的分力  、沿斜面向下的电场力 、沿斜面向上的弹簧弹力 三个力的作用。起初前两个力的合力大于弹簧的弹力，三力的合力沿斜面向下，物块加速下滑，下滑中弹力逐渐增大而其它两力不变，三力向下的合力越来越小，滑块的加速度减小，当合力小到等于零时，加速度为零，滑块的速度不再增加，达到最大值vm。设此时弹簧压缩量为x，对滑块在斜面方向运用共点力平衡条件有： 。滑块从释放到速度最大，滑块沿斜面下滑的距离为 ，斜面的弹力不做功，重力的功为 ，电场力的功为 ，设弹簧的弹力所做的功为Ｗ，对滑块这一运动过程运用动能定理有： ，解得： 。【点评】加速度减小的加速直线运动中，加速度为零时，速度最大。 6．涉及磁场的力电综合问题 闭合电路的一部分导体在磁场中做切割磁感线运动时，由于电磁感应，导体中出现电流，磁场对载流导体的安培力将做功，系统的机械能不守恒。这类问题可运用动能定理或能量守恒定律分析求解。 例6．如图6所示，两足够长的光滑金属导轨竖直放置，相距为L，一理想电流表与两导轨相连，匀强磁场与导轨平面垂直。一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放。导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为I。整个运动过程中，导体棒与导轨接触良好，且始终保持水平，不计导轨的电阻。求： （1）电流稳定后，导体棒运动速度的大小； （2）若从导体棒进入磁场区域到开始匀速运动，下落的距离为H，安培力的功。 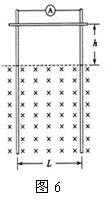  解析：（1）在进入磁场区域前，导体棒自由落体运动，进入磁场后，由法拉第电磁感应定律有：  ，由欧姆定律有： ，由安培力公式有： 。导体刚进入磁场运动时所受向上的安培力小于向下的重力，做加速运动，随速度的增加安培力增加，导体棒运动的加速度越来越小，当安培力增大到等于重力，加速度为零，速度不再增加，电流保持稳定。此时有： 。解以上几式得，电流稳定后导体棒的运动速度为： 。（2）设从导体棒进入到匀速运动，安培力的功为W，对导体棒从开始下落到匀速运动过程运用动能定理有：  ，解得： 。【点评】安培力随感应电流的变化而变化，在导体中的电流未恒定之前，安培力是变力，它的功只能依据动能定理或能量守恒定律分析求解。 (责任编辑：admin) |