|
分析天体问题的两个基本思路 江西省都昌县第一中学 李一新 天体有自然天体（如太阳、地球和月亮等）和人造天体（宇宙飞船、卫星和空间站等）两种，无论哪种天体，在分析天体问题时有两个基本思路。 思路一：不考虑某天体的自转，在该天体表面物体所受的重力等于天体对物体的万有引力。设某天体的质量为M，半径为R，表面处的重力加速度为g，物体的质量为m，则  ， 此式称为“黄金代换式”，可以把“地上”和“天上的问题联系起来。 思路二：行星（或卫星）的运动可看做匀速圆周运动，万有引力提供向心力。考虑天体的密度时，可将天体看作均匀的球体。 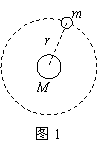 如图1所示，设某中心天体的质量为M，行星（或卫星）的质量为m，到中心天体的距离为r，则  。根据已知条件可选择合适的公式。例1．某课外小组长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R1，周期为T1，已知万有引力常量为G。求： （1）行星的质量； （2）若行星的半径为R，行星的第一宇宙速度是多少； （3）通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R2，周期为T2，试估算靠近行星周围众多卫星的总质量。 解析：（1）设行星的质量为M，离行星最近的卫星的质量为m，由万有引力定律和牛顿第二定律得  ，则行星的质量为： ①（2）卫星在行星表面环绕时，  ② 由①②两式得行星的第一宇宙速度：  ；（3）因为行星周围的卫星均匀分布，研究很远的卫星可把其它卫星和行星整体作为中心天体，设离行星很远的卫星的质量为m1，则  可得行星和其它卫星的总质量：  ，所以靠近该行星周围的众多卫星的总质量为： 。点评：关于天体的质量和运动速度等计算问题，一般都是通过思路二来分析的，有时也会综合应用二个思路。本题的关键点就是研究很远的卫星要把其它卫星和行星整体作为中心天体来整体分析。 例2．已知地球半径为R，一只静止在赤道上空的热气球（不计气球离地高度）绕地心运动的角速度为ω0，在距地面h高处的圆形轨道上，有一颗人造地球卫星，设地球质量为M，热气球的质量为m，人造地球卫星的质量为m1，根据以上条件，有一位同学列出了以下两个式子： 对热气球：  ①对人造地球卫星：  ②进而求出了人造地球卫星绕地球运行的角速度ω。你认为该同学的解法是否正确？若认为正确，请求出结果；若认为错误，请补充一个条件后，再求出ω。 解析：第①个式子（对热气球）不正确。因为热气球不同于人造地球卫星，热气球静止在空中是因为浮力与重力平衡，它绕地心运动的角速度等于地球自转角速度，向心力由万有引力的一部分提供，而不是全部。 情形一：若补充地球表面的重力加速度为g，不计气球离地高度，热气球受到的万有引力等于其重力，则 ③由②③两式联立可得  。情形二：若补充同步卫星的离地高度H，则  ④由②④两式联立可得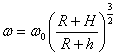：  。情形三：若补充第一宇宙速度v1，则  ⑤由②⑤两式联立可得：  。点评：此题是一道条件性开放题，由于万有引力恒量G未知，不能直接通过②式计算，需要补充条件才能计算，补充不同的条件可以有不同的解法，情形一补充条件利用了思路一，情形二和情形三补充条件利用了思路二。本题既能培养了学生判断纠错能力，又能培养了学生的发散性思维能力。 (责任编辑：admin) |