|
传动装置分析 江西省都昌县第一中学 李一新 皮带（链条）传动、齿轮传动和共轴传动，是常见的三种传动类型。在分析这些传动问题时，关键是寻找不变或相等的量。 一、皮带（链条）传动 如图1所示，A点和B点分别是两个轮子边缘上的点，两个轮子用皮带连接起来，并且皮带不打滑。其运动特点是它们的线速度大小相等 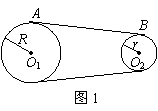 ，转动方向相同，角速度和周期与轮子半径的关系为： ， 。 二、齿轮转动 如图2所示，A点和B点分别是两个齿轮边缘上的点，两个齿轮用齿啮合。其运动特点是两个轮子在同一时间内转过的齿数相等，所以它们的线速度大小相等 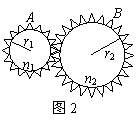，转动方向相反，角速度和周期与轮子半径和齿数的关系为： ， 。 三、共轴传动 如图3所示，A点和B点是在同轴转动的一个圆盘上两点，圆盘转动时，它们沿着不同的半径作圆周运动。其运动特点是它们的角速度大小相等 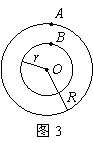 ，转动方向相同，周期和线速度与轮子半径的关系为： ， 。 例1．如图4所示，某种变速自行车有3个链轮和6个飞轮，链轮和飞轮的齿数如表1所示，该自行车的前后轮的直径为660mm，人骑自行车前进的速度为4m/s时，两轮不打滑，则脚踏板做匀速圆周运动的角速度最小值为：（ ） 
A.1.9rad/s B.3.5rad/s C.3.8rad/s D.7.1rad/s 解析 设链轮和飞轮的半径分别为r1和r2，齿数分别为N1和N2，转动的角速度分别为ω1和ω2，飞轮和后轮同轴转动，角速度相等，则：  。链轮和飞轮通过链条传动，线速度相等，则： ，解得 。由此可知，要使ω1最小，应同时使N1最大，N2最小，所以 ， ，代入上式可得 ，故正确的选项为B。例2．如图5所示，为一皮带传动装置，右轮的半径为r，a是它边缘上的一点；左侧是一轮轴，大轮的半径为4r，小轮的半径为2r，b点在小轮上，到小轮中心的距离为r，c点和d点分别位于小轮和大轮的边缘上，若在转动过程中，皮带不打滑，则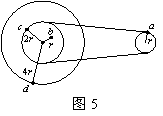（ ）  A. a点和b点的线速度大小相等 B. a点和b点的角速度大小相等 C. a点和c点的线速度大小相等 D. a点和d点的向心加速度大小相等 解析：a、c两点是皮带传动过程中的两点，皮带不打滑，它们的线速度大小相等，选项C正确；b、c两点是在同轮轴上，角速度相等，线速度与半径成正比，所以b、c两点的线速度大小不相等，故a、b两点的线速度大小也不相等，选项A错误；由于  ，得 ， ，所以选项B错误；由于 ，d点的向心加速度 ，a点的向心加速度 ，选项D正确，故正确的选项为C、D。
(责任编辑：admin) |
||||||||||||||||||||