|
轻杆、细线、弹簧的特性探究 武汉市青山区钢城十六中 朱广林 轻杆、细线、弹簧经常起着连接物体的作用，但由于它们的不同特性，表现出不同的力学特征。在物理学中，一般不计这三种物件的质量，可看成理想化的模型。 轻杆 轻杆的特性是不可变形的刚性杆，能对物体提供任意大小和方向的弹力。 例1 如图1所示，固定在小车支架上的斜杆与竖直杆的夹角为θ，在斜杆下端固定一个质量为m的小球，下列关于杆对球的作用力F的判断中，正确的是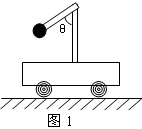（ ）  A．小车静止时，F=mgcosθ，方向沿杆向上 B．小车静止时，F=mgcosθ，方向垂直杆向上 C．小车向右以加速度a运动时，一定有F=mg/sinθ D．小车向左以加速度a运动时，一定有F=  ，方向斜向左上方，与竖直方向夹角α=arctan（a/g）解析：小车静止时，由物体的平衡条件知此时杆对球的作用力方向竖直向上，且大小等于球的重力mg，如图2所示。 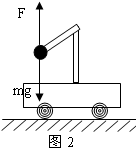 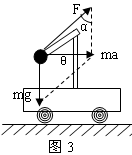 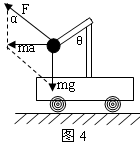 小车向右以加速度a运动时，杆对球的作用力F和重力的合力向右，大小为ma，由勾股定理得F= ，F与竖直方向夹角α=arctan（ma/mg）=arctan（a/g），α与θ不一定相等，如图3所示；同理，小车向左以加速度a运动时，F大小也是，与竖直方向夹角α=arctan（a/g），如图4所示。答案：D 例2 如图5所示，一轻杆BO，其O端用光滑铰链固定在竖直轻杆AO上，B端挂一重物，且系一细绳，细绳跨过杆顶A处的光滑小滑轮，用力F拉住。现将细绳缓慢往左拉，使杆BO与杆AO间的夹角逐渐减小，则在此过程中，拉力F及杆BO所受压力N的大小变化情况是（ ） A．N先减小，后增大 B．N始终不变 C．F先减小，后增大 D．F始终不变 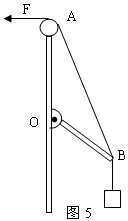 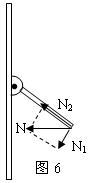 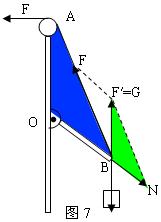 解析：轻杆一端与铰链连接后，轻杆可绕铰链端自由转动，轻杆在平衡时的受力只可能沿轻杆方向（拉力、压力均可），不可沿其它方向。现证明如下： 如图6所示，设轻杆的受力N不沿轻杆方向，可将N沿杆和垂直杆的方向进行正交分解，垂直杆的分力N1会使杆转动，不符合平衡的条件，因此杆受力只可能沿杆向内或向外。 此题受力分析如图7所示，B点受向下拉力（等于重物的重力）、绳的拉力、杆的支持力而平衡。将拉力F和支持力合成与向下的拉力平衡，由绿色的力三角形和蓝色的几何三角形相似，得  ，其中OA．OB．G都不变，所以N不变；AB减小，所以F减小。答案：B 细线、弹簧 细线产生微小形变，只能提供沿线收缩方向的拉力。 弹簧产生显著的弹性形变，可提供沿弹簧方向的拉力或压力。与细线一样，两端拉力一定大小相等。现证明如下： 如图8所示，设弹簧随两端连接的物体一起以加速度a运动，对弹簧用牛顿第二定律： F1－F2=ma，由于轻弹簧、细线都不计质量，m→0，所以合力ma=0，可得F1=F2。 胡克定律公式F=kx中，F指的是弹簧任意一端的拉力（压力）大小。 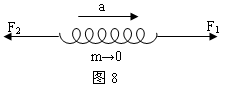 例3 如图9所示，四个完全相同的弹簧都处于水平位置，它们的右端受到大小皆为F的拉力作用，而左端的情况各不相同：①中弹簧的左端固定在墙上；②中弹簧的左端受大小同为F的拉力作用；③中弹簧的左端拴一小物块，物块在光滑的桌面上滑动；④中弹簧的左端拴一小物块，物块在有摩擦的桌面上滑动．若认为弹簧的质量都为零，以l1、l2、l3、l4依次表示四个弹簧的伸长量，则有( ) 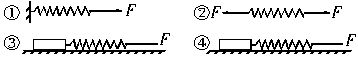 图9 A．l2>l1 B．l4>l3 C．l1>l3 D．l2=l4 解析：根据以上证明的结论，易知：当F相等时，弹簧的另一端必有一等大的力，弹簧的形变一定相同，与另外一端连接的物体无关，也与运动状态无关。 答案：D 例4 如图10所示，甲、乙重物均处于静止状态。当分别剪断细线的瞬间，关于小球的加速度的说法中，正确的是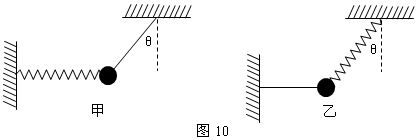（ ）  A．a甲=g/cosθ，方向沿绳的反方向；a乙=gtanθ，方向向右 B．a甲=gcosθ，方向沿绳的反方向；a乙=g/sinθ，方向向左 C．a甲=gtanθ，方向向右；a乙=gctgθ，方向向左 D．a甲=gctgθ，方向向右；a乙=gtanθ，方向沿绳的反方向 解析：剪断细线后，弹簧仍与小球相连。由于惯性，小球的位置不可能突变，弹簧的长度暂时不变，弹力的大小和方向仍然不变。即小球的合力为原来细线拉力的平衡力。 答案：A 小结：轻杆、细线、弹簧具有不同的力学特性，通过以上的一些证明和例题，希望对读者正确理解题意能有所帮助。若要有所提高，还需做一定量的练习，方能熟练。这类题目很多，限于篇幅，不再赘述。 (责任编辑：admin) |