|
一元二次方程解的情况在追及问题中的应用 江西省都昌县第一中学 李一新 应用数学知识解决物理问题的能力是高考考试说明中考查的五种能力之一。追及类问题是匀变速直线运动的综合应用，利用一元二次方程的解的情况分析，可以很方便地解决一些追及中的问题。 1．利用  判断是否相撞两物体追赶，后面的物体与前面的物体是否相撞，根据位移关系列出一个关于时间t的一元二次方程，若  ，方程有解，两物体相撞；若 ，方程无解，两物体不相撞。例1．在水平轨道上有两列火车A和B相距x，A车在后面做初速度为v0、加速度大小为2a的匀减速直线运动，而B车同时做初速度为零、加速度为a的匀加速直线运动，两车运动方向相同。要使两车不相撞，求A车的初速度v0满足的条件。 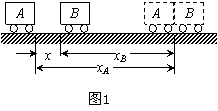 解析：如图1所示，设经过时间t两车相撞，则位移关系满足  ，即： 整理得3at2－2v0t＋2x＝0，这是一个关于时间t的一元二次方程，当判别式  时，t无实数解，即两车不相撞，所以要使两车不相撞，A车的初速度v0应满足的条件是v0≤。例2．经检测汽车A的制动性能：以标准速度20m/s在平直公路上行驶时，制动后40s停下来。现A在平直公路上以20m/s的速度行驶发现前方180m处有一货车B以6m/s的速度同向匀速行驶，司机立即制动，能否发生撞车事故？ 解析：汽车A的加速度为  ，设在t时刻两车相遇，由位移关系有： ，即：t2－56t＋720＝0。因Δ＝562－4×720＝256>0，故两车相撞。点评：匀减速直线运动追赶匀加速直线运动，当两者速度相等时，能追上，就一定能追上。 2．利用 判断相遇的次数两个物体追赶，有可能相遇有可能不相遇，相遇的次数是一次也有二次。利用位移关系列出一个关于时间t的一元二次方程，当  ，t有两个根，则两物体相遇二次；当 ，t只有一个根，则两物体相遇一次；当 方程无解，两物体不会相遇。例3．在平直的轨道上，甲、乙两车相距为x0，同向同时开始运动。甲在后面以初速度v1、加速度a1做匀加速度直线运动，乙在前面以初速度v2、加速度a2做匀加速度直线运动。假定甲能从乙的旁边通过而互不影响，下列情况说法正确的是：（ ） A.当a1＝a2时,甲、乙只能相遇一次 B.当a1＞a2时,甲、乙可能相遇二次 C.当a1＜a2时,甲、乙只能相遇二次 D.当a1＜a2时,甲、乙可能相遇二次 解析：  如图2所示，设经时间t，甲、乙相遇，由位移公式可得甲、乙两车的位移分别为：  ① ②相遇时位移关系满足：  ③由①②③三式可得方程：  ④分析与讨论： 1.当a1＝a2时，由④式可得  ，若v1＞v2，t＞0，能追上；若v1＜v2，t<0，不能追上。2.当a1≠a2时，由④式可得 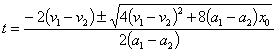 （1）当a1＞a2时,无论v1、v2的关系如何，t的两个解中都是一正一负，舍去负根，只有一个正根，即两车只能相遇一次。 （2）当a1＜a2时,若v1＜v2，t的两个解中均为负值，即两车不可能相遇。 若v1＞v2，当  时，t无解，即两车不可能相遇；当 时，t只有一解，即两车相遇一次；当 时，t有两个正解，即两车相遇二次。因此，此情形下两车有可能相遇和不相遇，相遇次数可能一次或二次。故正确的选项为AD。点评：利用上述方法，还可以分析以下几种相遇问题：①匀加速直线运动追赶匀速直线运动的情况；②匀减速直线运动追赶匀速直线运动的情况；③匀速直线运动追赶匀加速直线运动的情况；④匀速直线运动追赶匀减速直线运动的情况；⑤匀加速直线运动追赶匀减速直线运动的情况；⑥匀减速直线运动追赶匀加速直线运动的情况。 3．利用根的关系求解相遇时间 当两个物体相遇二次，从第一次相遇到第二次相遇要经过一段时间，根据位移关系列出一个关于时间t的一元二次方程， ，t有两个根，分别是两物体第一次和第二次相遇的时刻；则两物体相遇的时间为这两根之差。例4．如果公路上有一列汽车队以10m/s的速度正在匀速行驶，相邻车间的距离为25m，后面有一辆摩托车以20m/s的速度同向行驶，当它距离车队最后一辆车距离为25m时刹车，以0.5m/s2的加速度做匀减速运动，摩托车在车队旁边行驶而过。设车队车辆数n足够多，求： （1）摩托车最多与几辆汽车相遇？最多与车队汽车相遇几次？ （2）摩托车从赶上车队到离开车队，共经历多长时间？ 解析：（1）设摩托车的速度与汽车的速度相等时经历的时间为t，车队的速度和摩托车的初速度用v1和v2表示，由速度公式可得：  ，即 ，摩托车前进的距离为： ，车队前进的距离为：   将车队从车尾依次编号为1、2、3……n，如图3所示，设摩托车最多与n辆汽车相遇，由位移关系可得：  。解得： 即摩托车最多与4辆汽车相遇，相遇后摩托车的速度继续减小，车队后面汽车又陆续超过摩托车，故摩托车最多与车队中汽车相遇7次。 （2）设摩托车经时间t‘与车队最后一辆汽车相遇，则：  。代入数据整理得： 。 ，且方程有两个正根，分别为 和 ，此两个根正是摩托车先赶上车队到又离开车队的两个时刻，所以摩托车从赶上车队到离开车队，经历时间为此方程的两个根之差。 。点评：摩托车从赶上车队到离开车队的过程是，先是摩托车追上车队最后一辆汽车，然后是追上车队倒数第四辆汽车，再是车队最后一辆汽车离开摩托车。此题亦可以把上述各个过程中经历的时间计算出来，再计算出摩托车从赶上车队到离开车队经历的时间。 (责任编辑：admin) |