|
重新审视出新意 ──用基本公式求解匀变速直线运动问题 江苏省靖江市季市中学 范晓波 匀变速直线运动的基本规律,属高考II级要求,也是高中物理中研究所有与运动有关的问题的基础。在高考中单独考查的情况不多,主要以与曲线运动、电场、磁场等知识综合的形式出现,因此,高一学习时就必须非常熟悉各条规律并能灵活运用,为将来的综合解题做准备。这部分由于涉及的公式较多,实际问题的情境也会不断变化,这些都给初学者带来不小的困难。但若能从物理量的特点出发,重新审视各表达式的内涵,就能化解难点,事半功倍。下面先就如何运用三个基本运动规律 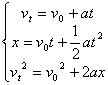 (其实 (其实一、运动学量巧分类 初速度 二、基本公式重命名 在速度公式 三、选择的思路与方法 常见的匀变速直线运动问题按涉及的物理量种类可分为三种: 1.已知两个常量和一个变量的问题 例:骑自行车的人以5m/s的初速度匀减速上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?  分析:了解过程特点后分两行列出常量与相关变量,未知量后面做好标记。如下 常量 变量 题中 解:选择初速度方向为正方向, 由位移公式 解得 其中 说明:此类问题的处理比较简单,直接选用未知变量与已知变量间的关系式即可。 2.已知一个常量和两个变量的问题 例:飞机着陆后做匀变速直线运动,速度逐渐减小,已知飞机着陆时的速度为 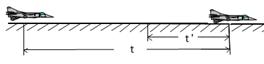 分析:在飞机着陆的整个过程中 常量 变量 要想求出运动时间 在飞机着陆前5 s运动过程中 常量 变量 明显可以对前5s过程运用 解:选择飞机滑行方向为正方向 在飞机着陆前5 s内,由 在飞机着陆的整个过程中,由 所以飞机继续滑行时间 说明:此类问题一般先利用两个已知变量间的关系式求出未知常量,再利用未知变量与任一已知变量间的关系式解决问题。 3.两个常量均未知的问题 例:一辆汽车在平直公路上匀速行驶,因前方有障碍物司机立即刹车,  分析:常量 变量 此过程最明显的特征是 解:选择汽车行驶方向为正方向 由  解得: 即汽车刹车后加速度大小为 说明:此类问题属用基本运动规律解决匀变速直线运动问题中比较复杂的一种,一般需选择两个关系式列方程组求解,而且考虑到运算的方便, 原则上,仅利用基本公式已经可以解决一切匀变速直线运动的问题,但对其中很多实际问题,求解过程比较繁琐,如能结合基本公式的相关推论或典型问题的解题技巧进行讨论,可以大大简化处理过程,做到省时又省力。 四、变式练习 1.物体的初速度为2 m/s,加速度为2 m/s2,当它的速度增加到6 m/s时,所通过的位移是多少? 2.已知一小球做初速度为0的匀加速直线运动,小球在第2s内通过位移为3m,求小球在5s内通过的位移是多少? 3.一个骑自行车的人想依靠惯性冲上一个斜坡,已知上冲时的加速度大小是0.4m/s2,斜坡长20m,求骑自行车的人到达斜坡顶端最多需要多长时间? 4.一物体作匀变速直线运动,第3s内的位移为 5.马路旁每两根电线杆间的距离都是60m,坐在汽车里的乘客测得汽车从第1根电线杆驶到第2根电线杆用了5s,从第2根电线杆驶到第3根电线杆用了3s.如果汽车是匀加速行驶的,求汽车的加速度和经过这三根电线杆时的瞬时速度的大小。 变式练习答案: 1. 2. 3. 4. 5. |
