|
对象不同 用法有异 ──谈机械能守恒定律的应用 江苏省靖江市季市中学 范晓波 能量转化和守恒定律是自然界四大基本规律之一,机械能守恒定律又是能量守恒定律在机械运动中的具体表现形式,由于机械能守恒定律不涉及运动过程中的加速度和时间,用它来处理动力学问题要远比牛顿运动定律方便。机械能守恒定律适用的对象可以是单个物体(弹簧)和地球组成的系统,也可以是多个物体(弹簧)和地球组成的系统。不过,对象不同,在守恒的判断上、运用的方式上略有差异。 机械能包括动能、重力势能和弹性势能三种,由于重力势能属于物体和地球组成的系统,因此,只要涉及重力势能,地球就必定是研究对象的一部分,也正因为如此,在交代研究对象时地球可以不特别指明。 一、单个物体(弹簧)和地球组成的系统 机械能守恒条件: (1)只受重力或系统内弹簧弹力;(注意:从研究对象的组成可知,重力也属内力) (2)受其它外力,但其它外力不做功; (3)其它外力做功,但其它外力做功的代数和始终为0。 满足上述三个条件中任何一个,该系统的机械能都守恒。其中第三个条件需要进行一点补充说明,以沿水平公路匀速直线运动的汽车为例,运行过程中,发动机内部燃烧汽油,一部分化学能转化为机械能,同时,汽车克服阻力做功,一部分机械能又转化为内能,两个转化过程中机械能变化的数值相等,因此汽车机械能的总量保持不变。正因如此,严格地讲,第三个条件不属于机械能守恒的条件之列,只是研究过程中机械能的数值始终保持不变而已。 例:如图所示,小球从某一高处自由下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的过程中,下列关于机械能的叙述中正确的是( )  (A)重力势能和动能之和总保持不变 (B)重力势能和弹性势能之和总保持不变 (C)动能和弹性势能之和总保持不变 (D)重力势能、弹性势能和动能之和总保持不变 分析:这是一个经典问题,难点在于研究对象的选择。若以小球、地球组成的系统为对象,弹簧弹力属于外力,系统机械能不守恒;若以小球、弹簧、地球组成的系统为对象,弹簧弹力属于内力,系统机械能守恒。 解:应选D选项。 说明:涉及弹簧的问题一定要注意弹簧是否为系统的组成部分,因为这将决定弹簧弹力到底属于内力还是外力,有没有外力对系统做功,系统的机械能是否守恒? 例:如图所示,均匀铁链长为  分析:将铁链与地球组成一个系统,由于桌面的弹力对铁链不做功,只有重力做功,因此系统的机械能守恒。另外,铁链下落前,形状不规则,重力势能最好分段计算,但要注意质量的对应性。 解:选取桌面为零势能面,对铁链与地球组成的系统由机械能守恒定律可得: 即 解得: 说明:此题也可选取地面为零势能面求解。零势能面选取不同,列出的表达式不同,虽然最后解得的结果是一样的,但解方程时的简易程度明显不同。因此,灵活、准确地选取零势能面,往往会给题目的求解带来方便。如果想避开零势能面的选取,可考虑使用 二、多个物体(弹簧)和地球组成的系统 机械能守恒的条件: (1)系统外部无作用力对系统内部物体做功 (2)系统内部无滑动摩擦力、流体的阻力、爆炸力等做功 必须同时满足这两个条件,该系统的机械能才守恒。而且系统的机械能应理解成内部包含的所有物体机械能的总和。当然处理实际问题时,往往有部分物体的部分种类能量没有发生变化,因此,对多个物体(弹簧)和地球组成的系统使用机械能守恒定律时,表达式写成 例:如图所示,一根长为  分析:设想 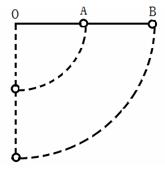 解: 又因为 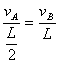 联立求解得: 说明:用 例:如图所示,一固定的楔形木块,其斜面的倾角 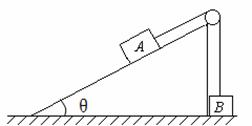 分析:细线断裂前, 解:设细线断裂瞬间, 则: 细线断裂后,设 则 所以 说明:与运动有关的连接体问题一般优先从能量的角度进行分析。对连接体和地球组成的系统,分别检查外力和内力做功的情况,满足机械能守恒条件就使用机械能守恒定律,不满足则考虑使用能量守恒定律。 三、流体(或连续体)和地球组成的系统 借助等效的思想确定重力势能的变化量是处理流体(或连续体)问题常用的技巧。 例:如图所示,粗细均匀的 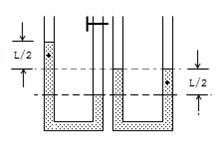 分析:由于摩擦阻力忽略不计,故水柱的机械能守恒。从初始状态到左右两管水面相平为止,相当于有长 解:如图,从打开阀门到左右水面刚好相平的过程中,整个水柱势能的减少量等效于高 设水柱总质量为 则 说明:本题在应用机械能守恒定律时仍然用 功能关系、机械能守恒定律是动力学和运动学知识的综合发展,一般运用在物理情境比较复杂的问题中,需要周密细致的分析受力情况、做功情况才能确保规律的使用万无一失。 变式练习: 1.如图所示,总长为 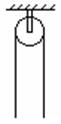 2.如图所示,一根长为  3.如图所示,半径为 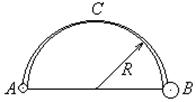 4.将细绳绕过两个定滑轮 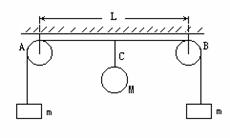 5.如图所示,游乐列车由许多节车厢组成。列车全长为 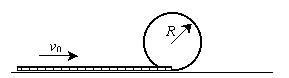 变式练习答案: 1.答案: 2.答案: 3.答案: 4.答案: 5.答案: |
