|
《3.3 直线的交点坐标与距离公式(2)》测试题 一、选择题 1.已知点O为原点,点P在直线 A.2 B. 考查目的:考查点到直线的垂线段最短的应用,以及点到直线的距离公式. 答案:C. 解析:由题意得, 2.(2011北京文)已知点A(0,2),B(2,0).若点C在函数 A.4 B.3 C.2 D.1 考查目的:考查点到距离公式的应用和数形结合的思想方法. 答案:A. 解析:直线AB的方程为 3.点M A.直线 考查目的:考查中点坐标公式,以及点与直线对称的有关性质. 答案:A. 解析:线段 二、填空题 4.若点O(0,0),A(4,-1)到直线 考查目的:考查点到直线的距离公式. 答案:-2或4或6. 解析:由题意得 5.若 考查目的:考查直线与直线的位置关系的应用. 答案:(9,-4). 解析:将直线方程 6.(2009全国Ⅰ文)若直线 考查目的:考查点到直线的距离公式,直线倾斜角与斜率的概念,以及分类讨论思想. 答案:①⑤. 解析:易求两条平行线 三、解答题 7.⑴已知直线 ⑵已知直线 考查目的:考查点关于直线的对称点的求法,两条直线关于某一条直线对称的点的性质,以及数形结合思想等. 答案:⑴(-2,7);⑵ 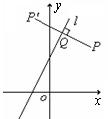 解析:⑴设点P关于直线 ∵ ∴直线 设 ∵Q是线段 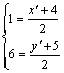 ,解得 ,解得∴点P关于直线 ⑵∵直线 ∴直线 易知点(0,-2)为直线 则 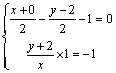 ,解得 ,解得由点A、B的坐标可求得,直线 8.直线 考查目的:考查中点坐标公式,两条直线的交点与方程组的解的关系,数形结合思想等. 答案: 解析:(方法一)设直线 (方法二)若直线 (责任编辑:admin) |
