|
《3.3 二元一次不等式(组)与简单的线性规划问题(2)》测试题 一、选择题 1.(2012安徽文)若 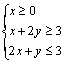 ,则 ,则A. 考查目的:考查线性规划的有关概念和求解方法,考查数形结合思想. 答案:A. 解析:约束条件对应的可行域为 2. (2010浙江理)若实数  ,且 ,且A. 考查目的:考查二元一次不等式组的平面区域,以及简单的转化思想和数形结合的思想. 答案:C. 解析:将最大值转化为目标函数 3.给出如图所示的平面区域,其中 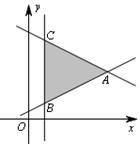 A. 考查目的:考查线性规划问题、直线的斜率公式等基础知识,考查数形结合和分析判断能力. 答案:B. 解析:目标函数 二、填空题 4.(2009山东文)某公司租赁甲、乙两种设备生产 考查目的:考查线性规划问题在实际中的应用. 答案:2300. 解析:设生产甲种设备需要 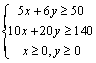 ,即: ,即: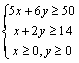 .作出可行域(图略).由 .作出可行域(图略).由5.(2012上海文)满足约束条件 考查目的:考查线性规划问题、作图能力和数形结合思想. 答案: 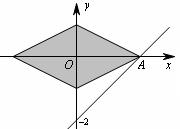 解析:根据题意得  ,或 ,或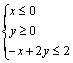 ,或 ,或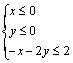 ,或 ,或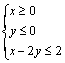 ,其可行域为平行四边形 ,其可行域为平行四边形6.(2012江苏卷)已知正数 考查目的:考查线性规划问题、直线的斜率概念与公式、导数的几何意义、直线的方程等基础知识,以及等价转化思想与数形结合思想. 答案: 解析:条件 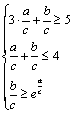 .设 .设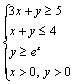 ,求 ,求 作出可行域如图所示(阴影部分), 三、解答题 7.某工厂生产甲、乙两种产品,计划每天每种产品的生产量不少于15吨,已知生产甲产品1吨需煤9吨,电力4千瓦时,劳力3个;生产乙产品1吨需煤4吨,电力5千瓦时,劳力10个;甲产品每吨的利润为7万元,乙产品每吨的利润为12万元;但每天用煤不超过300吨,电力不超过200千瓦时,劳力只有300个. 问每天生产甲、乙两种产品各多少吨,才能使利润总额达到最大? 考查目的:考查线性规划问题、应用数学知识解决实际问题的能力. 答案:20,24. 解析:设每天生产甲、乙两种产品分别为 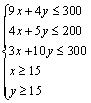 ,目标函数为 ,目标函数为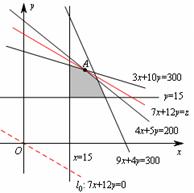 解方程组 答:每天应生产甲产品20吨,乙产品24吨,才能使利润总额达到最大,为428万元. 8.(2010广东理)某营养师要为某个儿童预定午餐和晚餐. 已知一个单位的午餐含12个单位的碳水化合物6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C. 另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C. 如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐? 考查目的:考查二元一次不等式组表示的平面区域、线性规划问题等基础知识和方法,考查数形结合能力和应用数学知识解决实际问题的能力. 答案:4个单位的午餐、3个单位的晚餐. 解析:设该儿童分别预订 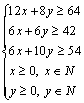 ,即 ,即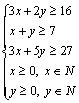 .作出可行域如图所示,并作出直线 .作出可行域如图所示,并作出直线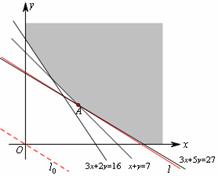 由方程组 答:应当为该儿童预订4个单位的午餐和3个单位的晚餐,既能满足营养要求,又可使花费最少. (责任编辑:admin) |
