第三章《不等式》复习测试题(一)
一、选择题
1.(2007上海理)设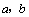 为非零实数,且 为非零实数,且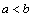 ,则下列不等式成立的是( ) ,则下列不等式成立的是( )
A.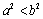 B. B. C. C.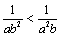 D. D.
考查目的:考查不等式的性质及“比较法”.
答案:C.
解析:∵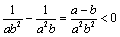 ,∴ ,∴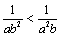 . .
2.已知 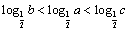 ,则( ). ,则( ).
A.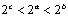 B. B.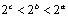 C. C. D. D.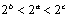
考查目的:考查指数(对数)函数单调性,了解不等式与函数单调性的关系.
答案:A.
解析:∵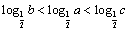 ,且函数 ,且函数 在 在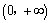 上是减函数,∴ 上是减函数,∴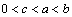 .又∵指数函数 .又∵指数函数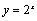 在 在 是是增函数,∴ 是是增函数,∴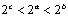 ,∴答案应选A. ,∴答案应选A.
3.(2009重庆理)不等式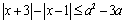 对任意实数 对任意实数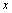 恒成立,则实数 恒成立,则实数 的取值范围是( ). 的取值范围是( ).
A. B. B.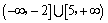 C. C. D. D.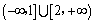
考查目的:考查绝对值的意义、函数的概念(或数形结合),以及一元二次不等式的解法.
答案:A.
解析:∵ 表示数轴上坐标为 表示数轴上坐标为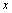 的点到坐标分别为 的点到坐标分别为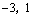 的两点的距离之差,∴对 的两点的距离之差,∴对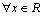 , , ,当 ,当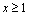 时, 时,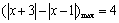 . ∵不等式 . ∵不等式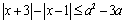 对任意实数 对任意实数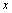 恒成立,∴ 恒成立,∴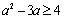 ,解得 ,解得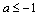 ,或 ,或 . .
4.(2008海南、宁夏)已知 ,则使得 ,则使得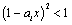  都成立的 都成立的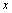 的取值范围是( ). 的取值范围是( ).
A.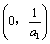 B. B.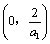 C. C. D. D.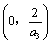
考查目的:考查一元二次不等式的解法、恒成立的不等式问题的处理方法.
答案:B.
解析:由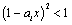 得, 得,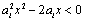 ,即 ,即 ,∴ ,∴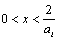 .∵此式对 .∵此式对 都成立,又∵ 都成立,又∵ ,∴ ,∴ . .
5.(2010四川理)设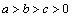 ,则 ,则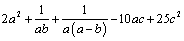 的最小值是( ). 的最小值是( ).
A.2 B.4 C. D.5 D.5
考查目的:考查运用基本不等式求最值的方法,以及等号成立的条件,考查分析问题解决问题的能力.
答案:B.
解析: 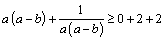 ,当且仅当 ,当且仅当 , , , ,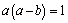 时等号成立,即当 时等号成立,即当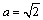 , ,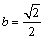 , ,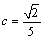 时, 时,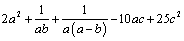 取得最小值4. 取得最小值4.
6.(2010重庆理)已知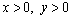 , ,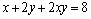 ,则 ,则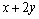 的最小值是( ). 的最小值是( ).
A.3 B.4 C. D. D.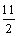
考查目的:考查均值不等式的应用.
答案:B.
解析:原等式可变形为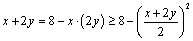 ,整理得 ,整理得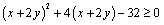 ,即 ,即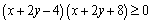 .又∵ .又∵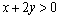 ,∴ ,∴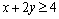 ,当且仅当 ,当且仅当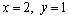 时取“=”号. 时取“=”号.
二、填空题
7.(2010福建理改编)设不等式组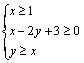 所表示的平面区域是 所表示的平面区域是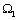 ,平面区域 ,平面区域 与 与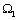 关于直线 关于直线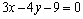 对称.对于 对称.对于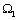 中的任意一点A与 中的任意一点A与 中的任意一点B, 中的任意一点B,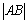 的最小值等于___________. 的最小值等于___________.
考查目的:考查简单的线性规划问题,以及点与直线之间的位置关系.
答案:4.
解析:由题意知,所求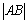 的最小值,即为区域 的最小值,即为区域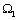 中点到直线 中点到直线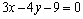 距离的最小值的两倍,画出已知不等式组表示的平面区域可以看出,点(1,1)到直线 距离的最小值的两倍,画出已知不等式组表示的平面区域可以看出,点(1,1)到直线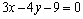 的距离最小,故 的距离最小,故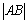 的最小值为 的最小值为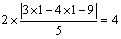 . .
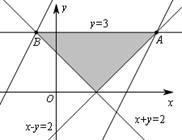
8.(2007福建理)已知实数 满足 满足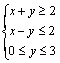 ,则 ,则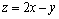 的取值范围是 . 的取值范围是 .
考查目的:考查简单的线性规划问题.
答案: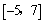 . .
解析:作出可行域如图所示,由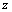 的几何意义可知,现行目标函数在点 的几何意义可知,现行目标函数在点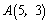 处取得最大值7,在点 处取得最大值7,在点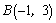 处取得最小值-5,所以 处取得最小值-5,所以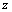 的取值范围是 的取值范围是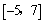 . .
9.(2012江苏卷)已知函数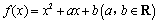 的值域为 的值域为 ,若关于 ,若关于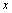 的不等式 的不等式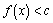 的解集为 的解集为 ,则实数 ,则实数 的值为 . 的值为 .
考查目的:考查二次函数、一元二次不等式等基础知识,考查运算求解能力.
答案:9.
解析:∵函数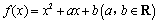 的值域为 的值域为 ,∴ ,∴ ①.∵不等式 ①.∵不等式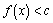 的解集为 的解集为 ,∴ ,∴ 是方程 是方程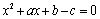 的两个根,∴ 的两个根,∴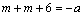 ②, ②, ③,由①③得 ③,由①③得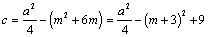 ,由②得, ,由②得, ,∴ ,∴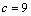 . .
10.(2011浙江理)设 为实数,若 为实数,若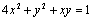 ,则 ,则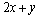 的最大值是 . 的最大值是 .
考查目的:考查基本不等式的应用和代数式的变形能力.
答案: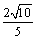 . .
解析: ,∴ ,∴ ,∴ ,∴ ,∴ ,∴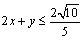 ,当且仅当 ,当且仅当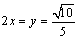 时取等号. 时取等号.
11.(2010安徽理)设 满足约束条件 满足约束条件 ,若目标函数 ,若目标函数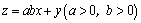 的最大值为8,则 的最大值为8,则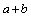 的最小值为________. 的最小值为________.
考查目的:考查简单的线性规划问题,基本不等式的应用.
答案:4.
解析:不等式表示的区域是一个四边形,4个顶点是(0,0),(0,2),(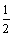 ,0),(1,4).易见目标函数在(1,4)处取得最大值8,∴ ,0),(1,4).易见目标函数在(1,4)处取得最大值8,∴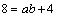 ,得 ,得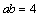 ,∴ ,∴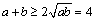 ,当且仅当 ,当且仅当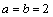 时取等号,∴ 时取等号,∴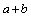 的最小值为4. 的最小值为4.
(责任编辑:admin) |
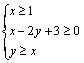 所表示的平面区域是
所表示的平面区域是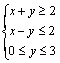 ,则
,则

 ,若目标函数
,若目标函数