|
《1.1 正弦定理和余弦定理(2)》测试题 一、选择题 1.(2010上海文)若 A.一定是锐角三角形. B.一定是直角三角形. C.一定是钝角三角形. D.可能是锐角三角形,也可能是钝角三角形. 考查目的:考查正弦定理、余弦定理. 答案:C 解析:由 2.(2011重庆理)若 A. 考查目的:考查余弦定理及代数式的变形能力. 答案:A. 解析:由 3.(2011四川理)在 A. 考查目的:考查正弦定理、余弦定理及余弦函数的单调性. 答案:C. 解析:由已知条件及正弦定理得 二、填空题 4.(2011全国新课标理) 考查目的:考查正弦定理或余弦定理、考查函数与方程思想以及运算求解能力. 答案: 解析:(方法一)根据正弦定理 (方法二)设角 5.在 考查目的:考查余弦定理以及代数式的变形能力. 答案:1. 解析:∵ 6.(2010江苏)在锐角 考查目的:考查正弦定理、余弦定理、三角函数知识的应用以及等价转化思想. 答案:4. 解析:(方法一)已知条件和所求结论对于角 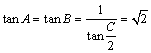 , ,(方法二)由 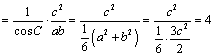 . .三、解答题: 7.(2007全国Ⅰ文)设锐角三角形 ⑴求 ⑵若 考查目的:考查正弦定理、余弦定理以及基本运算能力. 答案:⑴ 解析:⑴根据正弦定理,由 ⑵根据余弦定理,得 8. (2008重庆理)设 ⑴ 考查目的:考查正弦定理或余弦定理、三角函数的恒等变形以及运算求解能力. 答案:⑴ 解析:⑴由余弦定理得 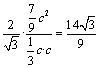 ,故 ,故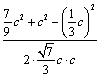 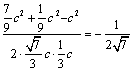 , ,(责任编辑:admin) |
