|
《2.3 等差数列的前n项和》测试题 一、选择题 1.(2008陕西卷)已知 A.64 B.100 C.110 D.120 考查目的:考查等差数列的通项公式与前 答案:B 解析:设 2.(2011全国大纲理)设 A.8 B.7 C.6 D.5 考查目的:考查等差数列通项公式的应用、前 答案:D 解析:由 3.(2012浙江理)设 A.若 C.若数列 D.若对任意 考查目的:考查等差数列的前 答案:C 解析:根据等差数列的前 二、填空题 4.(2011湖南理)设 考查目的:考查等差数列的性质及基本运算. 答案:81. 解析:设 5.(2008湖北理)已知函数 考查目的:考查等差数列的通项公式、前 答案: 解析:∵ 6.(2011广东理)等差数列 考查目的:考查等差数列的性质及基本运算. 答案:10. 解析:设等差数列 三、解答题 7.设等差数列 ⑴ ⑵ 考查目的:考查等差数列通项公式、前 答案:⑴ 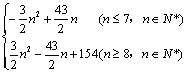 解析:设等差数列 ⑴ ⑵由 当 当 ∴ 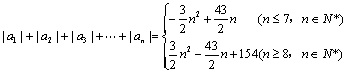 8.(2010山东理)已知等差数列 ⑴求 ⑵令 考查目的:考查等差数列的通项公式与前 答案:⑴ 解析:⑴设等差数列 ⑵由⑴知 (责任编辑:admin) |
