|
南昌市高中新课程训练题(不等式1) 命题人:南昌一中 喻瑞明 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.已知集合M=|x|x2<4|,N=|x|x2-2x-3<0|,则集合M A. C.{x|-1<x<2 2.设a、b、c是互不相等的正数,则下列等式中不恒成立的是( ) A. C. 3.如果 ① A.2 B.3 C.4 D.5 4.若 A.A≤G≤H B.A≤H≤G C.H≤G≤A D.G≤H≤A 5.已知 A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件 6. 设,y∈R,且x A. 2- 7.若不等式x2+ax+1?0对于一切x?(0, A.0 B. –2 C.- 8.下列结论正确的是 ( ) A.当 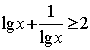 ; B.当 ; B.当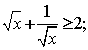 C.当 9.f (x)=3ax—2a+1若存在 A.-1<a< 10. f (x)= A. 11.关于x的不等式ax—b>0的解集是( A. C.(1,2) D. 12.若a,b,c>0且a(a+b+c)+bc=4-2 (A) (C) 2 二、填空题:本大题共4小题,每小题4分,共16分。请把答案填在答题卡上。 13.b克糖水中有a克糖(b>a>0),若再加入m克糖(m>0),则糖水更甜了,试根据这个事实写出一个不等式 。 14.设a,b是两个实数,给出下列条件:①a+b>1; ②a+b=2;③a+b>2;④a 15.不等式(x—2) 16.不等式 三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。 17.已知 18..设 19.解关于x的不等式 20.已知不等式 (I)求t,m的值; (2)若函数f(x)=-x2+ax+4在区间 21.设函数 (1)求函数 (2)若当 22.已知函数 (1)如果函数 (2)研究函数 (3)对函数 参考答案 一、选择题
二、填空题 13、 15、 三、解答题 17、解: 一. 二. 18.证: 要证明原不等式成立,则只要证: 只要证: 若 若1+ab>0,则只要证: 只要证: 上式显然成立,从而原不等式成立。 19、解:原不等式化为 ⑴当 a>0时,(*)等价于 ∴不等式的解为: ⑵当a=0时,(*)等价于 ⑶当a<0时,(*)等价于 ∴ 不等式的解为 : x<1或x> 综上所述:当a>0时,不等式的解集为( 当a<0时,不等式的解集为 20、解:⑴ ⑵ 又 由 由 由 故原不等式的解集为 21.(1) 由表
可知 (2)由 而 故 所以 22.解(1) 函数y=x+ (2)设0<x1<x2,y2-y1= 当 当0<x1<x2< 又y= (3)可以把函数推广为y= 当n是奇数时,函数y= 在(-∞,- 当n是偶数时,函数y= 在(-∞,- F(x)= = 因此F(x) 在 [ 所以,当x= 当x=1时F(x)取得最小值2n+1. (责任编辑:admin) |
