|
2.1数列的概念与简单表示 重难点：理解数列的概念，认识数列是反映自然规律的基本数学模型，探索并掌握数列的几种间单的表示法（列表、图象、通项公式）；了解数列是一种特殊的函数；发现数列规律找出可能的通项公式． 考纲要求：①了解数列的概念和几种简单的表示方法(列表、图像、通项公式)． ②了解数列是自变量巍峨正整数的一类函数． 经典例题：假设你正在某公司打工，根据表现，老板给你两个加薪的方案：（Ⅰ）每年年末加1000元；（Ⅱ）每半年结束时加300元。请你选择:（1）如果在该公司干10年，问两种方案各加薪多少元？ （2）对于你而言，你会选择其中的哪一种？ 当堂练习： 1. 下列说法中，正确的是 ( ) A．数列1，2，3与数列3，2，1是同一个数列． B．数列l, 2，3与数列1，2，3，4是同一个数列. C．数列1，2，3，4，…的一个通项公式是an=n. D．以上说法均不正确． 2  巳知数列{ an}的首项a1=1，且an＋1=2 an＋1,(n≥2)，则a5为 ( )A．7． B．15 C．30 D．31． 3.数列{ an}的前n项和为Sn=2n2＋1，则a1,a5的值依次为 ( ) A．2，14 B．2，18 C．3，4． D．3，18． 4.已知数列{ an}的前n项和为Sn=4n2 －n＋2，则该数列的通项公式为 ( ) A． an=8n＋5(n∈N*) B． an=8n－5(n∈N*) C． an=8n＋5(n≥2) D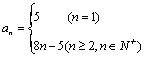．  5.已知数列{ an}的前n项和公式Sn=n2＋2n＋5，则a6＋a7＋a8= ( ) A．40． B．45 C．50 D．55． 6.若数列  前8项的值各异，且 对任意的 都成立，则下列数列中可取遍前8项值的数列为 （ ）A.  B. C. D. 7.在数列{ an}中，已知an=2，an= an＋2n，则a4 +a6 +a8的值为 ． 8.已知数列{ an}满足a1=1 ， an＋1=c an＋b, 且a2 =3,a4=15,则常数c,b 的值为 . 9.已知数列{ an}的前n项和公式Sn=n2＋2n＋5，则a6＋a7＋a8= ． 10.设  是首项为1的正项数列，且 （ =1，2，3，…），则它的通项公式是 =________．11. 下面分别是数列{ an}的前n项和an的公式，求数列{ an}的通项公式： (1)Sn=2n2-3n； (2)Sn=3n-2 12. 已知数列{ an}中a1=1，  (1)写出数列的前5项；(2)猜想数列的通项公式．13. 已知数列{ an}满足a1=0，an＋1＋Sn=n2＋2n(n∈N*)，其中Sn为{ an}的前n项和，求此数列的通项公式． 14. 已知数列{ an}的通项公式an与前n项和公式Sn之间满足关系Sn=2－3an (1)求a1; (2)求an与an (n≥2，n∈N*)的递推关系； (3)求Sn与Sn (n≥2，n∈N*)的递推关系， 参考答案： 经典例题：解：（1）（Ⅰ）55000元（Ⅱ）63000元 （2）当n<2时（Ⅰ）方案 当n=2时（Ⅰ）（Ⅱ）方案都行 当n<2时（Ⅱ）方案 当堂练习： 1.C; 2.C; 3.D; 4.D; 5.B; 6.B; 7. 46; 8.  或 ; 9. 45; 10.  ; 11. 【 解】 (1) an=4n+5 (2) 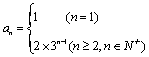 12. 【 解】 (1)1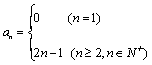,  ,  , , .(2).13. 【 解】  14. 【 解】 (1) (2) an +1= an (n≥1,n∈N*)(3) Sn +1=Sn+ (n≥1,n∈N*) (责任编辑：admin) |