|
2.2等差数列、等比数列 重难点：理解等差数列、等比数列的概念，掌握等差数列、等比数列的通项公式与前  项和公式，能在具体的问题情境中，识别数列的等差关系或等比关系，并能用有关知识解决相应的问题．考纲要求：①理解等差数列、等比数列的概念． ②掌握等差数列、等比数列的通项公式与前 项和公式．③能在具体的问题情境中，识别数列的等差关系或等比关系，并能用有关知识解决相应的问题． ④了解等差数列与一次函数、等比数列与指数函数的关系． 经典例题：已知一个数列{an}的各项是1或3．首项为1，且在第k个1和第k+1个1之间有2k-1个3，即1，3，1，3，3，3，1，3，3，3，3，3，1，…，记该数列的前n项的和为Sn． （1）试问第2006个1为该数列的第几项？ （2）求a2006； （3）求该数列的前2006项的和S2006； 当堂练习： 1．数列  则 是该数列的（ ）A．第6项 B．第7项 C．第10项 D．第11项 2．方程  的两根的等比中项是（ ）A．  B． C． D． 3． 已知  为各项都大于零的等比数列，公比 ，则（ ）A．  B． C．  D． 和 的大小关系不能由已知条件确定4．一个有限项的等差数列，前4项之和为40，最后4项之和是80，所有项之和是210，则此数列的项数为（ ） A．12 B．  C．16 D．185．若a、b、c成等差数列，b、c、d成等比数列，  成等差数列，则a、c、e成（ ）A．等差数列 B．等比数列 C．既成等差数列又成等比数列 D．以上答案都不是 6．在等差数列{an}中，  ，则 （ ）A．4 B．  C．8 D． 7．两等差数列{an}、{bn}的前n项和的比  ，则 的值是（ ）A．  B． C． D． 8．{an}是等差数列，  ，则使 的最小的n值是（ ）A．5 B．  C．7 D．89．{an}是实数构成的等比数列，  是其前n项和，则数列{} 中（ ）A．任一项均不为0 B．必有一项为0 C．至多有一项为0 D．或无一项为0，或无穷多项为0 10．某数列既成等差数列也成等比数列，那么该数列一定是（ ） A．公差为0的等差数列 B．公比为1的等比数列 C．常数数列  D．以上都不对11．已知等差数列{an}的公差d≠0，且a1、a3、a9成等比数列，则  的值是 ．12．由正数构成的等比数列{an}，若  ，则 ．13．已知数列{an}中，  对任意正整数n都成立，且 ，则 ．14．在等差数列{an}中，若  ，则有等式 成立，类比上述性质，相应地：在等比数列{bn}中，若 ，则有等式 15． 已知数列{2n-1an }的前n项和  ．⑴求数列{an}的通项公式；⑵设  ，求数列 的前n项和．16．已知数列{an}是等差数列，且  ．⑴求数列{an}的通项公式；⑵令  ，求数列{bn}前n项和的公式．17． 甲、乙两人连续6年对某县农村养鸡业规模进行调查，提供两个不同的信息图如图所示．甲调查表明:从第1年每个养鸡场出产1万只鸡上升到第6年平均每个鸡场出产2万只鸡．乙调查表明:由第1年养鸡场个数30个减少到第6年10个． 请您根据提供的信息说明： ⑴第2年养鸡场的个数及全县出产鸡的总只数； ⑵到第6年这个县的养鸡业比第1年是扩大了还是 缩小了？请说明理由； ⑶哪一年的规模最大？请说明理由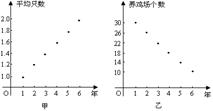．  18．已知数列{an}为等差数列，公差  ，{an}的部分项组成的数列 恰为等比数列，其中 ，求 ．参考答案： 经典例题：(1)4022031 (2)3 (3)5928 当堂练习： 1.B; 2.B; 3.A; 4.B; 5.B; 6.B; 7.B;8.B; 9.D; 10.B; 11.  1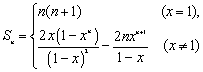2. 7 13. 1 14.  15. (1)  (2) 16. (1)  (2)  17．(1) 第2年养鸡场的个数为26个，全县出产鸡的总只数是31.2万只 (2) 到第6年这个县的养鸡业比第1年缩小了 (3) 第2年的规模最大 18．  (责任编辑：admin) |