|
第二章《数列》测试题(二) 三、解答题 12.(2009浙江文)设 ⑴求 ⑵若对于任意的 考查目的:考查数列的通项与前 答案:⑴ 解析:⑴当 ⑵∵ 13.(2010全国卷Ⅱ文)已知 ⑴求 ⑵设 考查目的:考查等比数列的通项公式与前 答案:⑴ 解析:⑴设 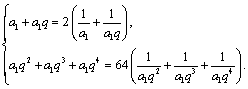 , ,化简得 ⑵由⑴知 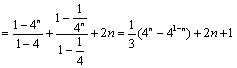 . .14.(2008湖南理)数列 ⑴求 ⑵设 考查目的:考查数列递推公式的运用、等差数列、等比数列的概念和通项公式、三角函数等基础知识,考查数列求和、不等式证明的基本方法,以及分析问题解决问题的能力. 答案:⑴ 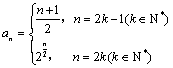 ;⑵略. ;⑵略.解析:⑴∵ 一般地,当 当 ∴数列 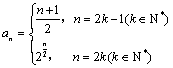 . .⑵由⑴知, 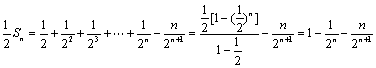 ,∴ ,∴要证明当 证明:要证明 ∴当 15.(2012广东理)设数列 ⑶证明:对一切正整数 |

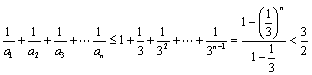 .
.