|
2.1-2椭圆 重难点：建立并掌握椭圆的标准方程，能根据已知条件求椭圆的标准方程；掌握椭圆的简单几何性质，能运用椭圆的几何性质处理一些简单的实际问题． 经典例题：已知A、B为椭圆  + =1上两点，F2为椭圆的右焦点，若|AF2|+|BF2|= a，AB中点到椭圆左准线的距离为 ，求该椭圆方程．当堂练习： 1．下列命题是真命题的是 （ ） A．到两定点距离之和为常数的点的轨迹是椭圆 B．到定直线  和定点F(c，0)的距离之比为 的点的轨迹是椭圆C．到定点F(－c，0)和定直线  的距离之比为(a>c>0)的点的轨迹 是左半个椭圆D．到定直线 和定点F(c，0)的距离之比为 (a>c>0)的点的轨迹是椭圆2．若椭圆的两焦点为（－2，0）和（2，0），且椭圆过点  ，则椭圆方程是 （ ）A．  B． C． D． 3．若方程x2+ky2=2表示焦点在y轴上的椭圆，则实数k的取值范围为 （ ） A．（0，+∞） B．（0，2） C．（1，+∞） D．（0，1） 4．设定点F1（0，－3）、F2（0，3），动点P满足条件  ，则点P的轨迹是（ ）A．椭圆 B．线段 C．不存在 D．椭圆或线段 5．椭圆  和  具有 （ ）A．相同的离心率 B．相同的焦点 C．相同的顶点 D．相同的长、短轴 6．若椭圆两准线间的距离等于焦距的4倍，则这个椭圆的离心率为 （ ） A．  B． C． D．  7．已知  是椭圆 上的一点，若到椭圆右准线的距离是 ，则点到左焦点的距离（ ）A．  B． C． D． 8．椭圆  上的点到直线 的最大距离是 （ ）A．3 B．  C． D． 9．在椭圆  内有一点P（1，－1），F为椭圆右焦点，在椭圆上有一点M，使|MP|+2|MF|的值最小，则这一最小值是 （ ）A．  B． C．3 D．410．过点M（－2，0）的直线m与椭圆  交于P1，P2，线段P1P2的中点为P，设直线m的斜率为k1（ ），直线OP的斜率为k2，则k1k2的值为 （ ）A．2 B．－2 C．  D．－11．离心率  ，一个焦点是 的椭圆标准方程为 ___________ .12．与椭圆4 x 2 + 9 y 2 = 36 有相同的焦点,且过点(－3，２)的椭圆方程为_______________． 13．已知  是椭圆 上的点，则 的取值范围是________________ ．14．已知椭圆Ｅ的短轴长为6，焦点Ｆ到长轴的一个端点的距离等于９，则椭圆Ｅ的离心率等于__________________． 15．已知椭圆的对称轴为坐标轴，离心率  ，短轴长为 ，求椭圆的方程．16．过椭圆  引两条切线PA、PB、A、B为切点，如直线AB与x轴、y轴交于M、N两点． （1）若  ，求P点坐标；（2）求直线AB的方程（用  表示）；（3）求△MON面积的最小值．（O为原点） 17．椭圆   ＞ ＞ 与直线 交于、 两点，且 ，其中 为坐标原点.（1）求  的值；（2）若椭圆的离心率  满足 ≤≤ ，求椭圆长轴的取值范围.18．一条变动的直线L与椭圆  + =1交于P、Q两点，M是L上的动点，满足关系|MP|·|MQ|=2．若直线L在变动过程中始终保持其斜率等于1．求动点M的轨迹方程，并说明曲线的形状．参考答案： 经典例题：[解析]：设A(x1，y1)，B(x2，y2)，  由焦半径公式有a－ex1+a－ex2= ，∴x1+x2= ，即AB中点横坐标为  ，又左准线方程为 ，∴ ，即a=1，∴椭圆方程为x2+ y2=1．当堂练习： 1.D; 2.D; 3.D; 4.A; 5.A; 6.D; 7.B; 8.D; 9.C; 10.D; 11.  ; 1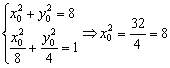2.  ; 13.  ;14.  ; 16．[解析]：（1）  ∴OAPB的正方形由   ∴P点坐标为（ ）（2）设A（x1，y1），B（x2，y2） 则PA、PB的方程分别为  ，而PA、PB交于P（x0，y0）即x1x0+y1y0=4，x2x0+y2y0=4，∴AB的直线方程为：x0x+y0y=4 （3）由  、    当且仅当  .17． [解析]：设  ，由OP ⊥ OQ  x 1 x 2 + y 1 y 2 = 0 又将   ，  代入①化简得  .(2)  又由（1）知  ，∴长轴 2a ∈ [ ].18．[解析]：设动点M(x，y)，动直线L：y=x+m，并设P(x1，y1)，Q(x2，y2)是方程组  的解，消去y，得3x2+4mx+2m2－4=0，其中Δ=16m2－12(2m2－4)>0，∴－ <m<，且x1+x2=－ ，x1x2= ，又∵|MP|= |x－x1|，|MQ|=|x－x2|．由|MP||MQ|=2，得|x－x1||x－x2|=1，也即|x2－(x1+x2)x+x1x2|=1，于是有  ∵m=y－x，∴|x2+2y2－4|=3．由x2+2y2－4=3，得椭圆 夹在直线 间两段弧，且不包含端点．由x2+2y2－4=－3，得椭圆x2+2y2=1．(责任编辑：admin) |