|
3.1复数的概念 重难点：理解复数的基本概念；理解复数相等的充要条件；了解复数的代数表示法及其几何意义． 考纲要求：①理解复数的基本概念． ②理解复数相等的充要条件． ③了解复数的代数表示法及其几何意义． 经典例题： 若复数  ，求实数 使 。（其中 为 的共轭复数）．当堂练习： 1.  是复数 为纯虚数的（ ）A．充分条件 B.必要条件 C.充要条件 D.非充分非必要条件 2  设 ，则 在复平面内对应的点位于（ ）A.第一象限 B.第二象限 C.第三象限 D.第四象限 3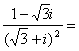．  （ ） A．  B． C． D． 4．复数z满足  ，那么 ＝（ ）A．2＋i B．2－i C．1＋2i D．1－2i 5.如果复数  的实部与虚部互为相反数，那么实数b等于（ ） A. B. C.2 D.－ 6.集合｛Z︱Z＝  ｝，用列举法表示该集合，这个集合是（ ）A｛0，2，－2｝ B.｛0，2｝ C.｛0，2，－2，2  ｝ D.｛0，2，－2，2，－2｝7.设O是原点，向量  对应的复数分别为 ，那么向量 对应的复数是（ ）    8、复数  ，则 在复平面内的点位于第（ ）象限。A．一 B.二 C.三 D .四 9.复数  不是纯虚数，则有（ ）    10.设i为虚数单位，则  的值为 （ ）A．4 B.－4 C.4i D.－4i 11.设  （为虚数单位），则z= ；|z|= . 12.复数  的实部为 ，虚部为 。13.已知复数z与 (z +2)2-8i 均是纯虚数,则 z = 14.设  ， ，复数 和 在复平面内对应点分别为A、B，O为原点，则 的面积为 。15. 已知复数z=(2+ )  ).当实数m取什么值时,复数z是:（1）零；（2）虚数；（3）纯虚数；（4）复平面内第二、四象限角平分线上的点对应的复数。  17． 设  R，若z对应的点在直线 上。求m的值。18． 已知关于  的方程组 有实数，求 的值。参考答案： 经典例题： 解析：由 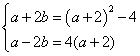，可知 ，代入得：  ，即   则  ，解得 或 。当堂练习： 1.B; 2.D; 3.B; 4.B; 5.D; 6.A; 7. B; 8.D; 9.C; 10.B; 11. 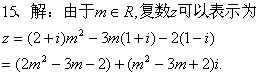 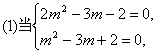， ; 12. 1， ;13.  ; 14. 1;    16．解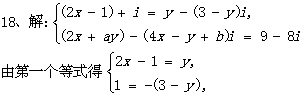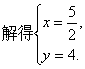：       将上述结果代入第二个等式中得  (责任编辑：admin) |