|
求解函数客观题的八种策略 广东省中山市第一中学 许少华 随着高考命题的改革，变一题把关为多题把关的特点更加突出。翻开近年的高考题，仔细看看选择题与填空题，也许你会感觉并非都是简单，更不是送分题。有些试题不是一般的难，而是相当难。当细心的看一下这些较难试题所涉及的知识点时，不禁大惊失色，怎么都是函数题？想一想也正常，函数具有抽象性、灵活性、应用性。仅这三大“性”，就可以设计出无穷多道，既有“华丽外表”又具“丰富内涵”的好题。那么，当我们面对这些“好题”时，该如何应对呢？本文教你“八招”，希望用它们可以铲除前进中的拦路“小题”。 1.特值开道 步步逼近 特值可以一个特殊数、也可以是一些特殊式子，它借助于“特殊性存在于一般性之中”这个哲学原理。通过特值开道，使看上去很难进行一般性求解的问题，在特值的“作用”下产生结论。 例1 设函数  在R上的导函数为 ,且 ，下面的不等式在R内恒成立的是A  B C D 解析：首先令  ，得 ，于是，排除B，D。再令  ，显然， 满足题设条件，此时， 不一定大于零，即选项C并非在R内恒成立，于是也被排除。故选A。点评：本题是特殊数与特殊式子齐“上阵”，使三个不合题意的选项被一一剔除，最终产生结论的。不否认此题存在一般性的推理、证明，但对于选择题来说，那么做会不会是“小题大做”呢？ 例2 已知函数 是定义在实数集 上的不恒为零的偶函数，且对任意实数 都有 ，则 的值是 A.0 B.  C.1 D. 解析：令  ，得 ，结合是定义在实数集上的不恒为零的偶函数，得 ；再令，得 由 得 ，再令  ，得 ；再令 ，得 ；那么  于是选A。点评：看上去多么“惊心动魄”啊！特殊值一个连一个、一环扣一环，在紧张、肃穆 的考场上，你能运用自如吗？本题还极具“诱误”性，请看由 得 你会不会猜测 ，从而产生答案D呢？2.巧构方程 层层深入 方程思想是重要的数学思想，方程与函数又是一对“密友”，函数中藏着方程、方程里含着函数是常有的事。遇到递推或含有明显变量的式子，想一想方程是应该的，也许它引领你层层深入，最终产生结论。 例3 定义在R上的函数 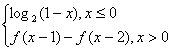满足  ，则 的值为( )A.-1 B. 0 C.1 D. 2 解析：由  ，得 两式相加得 ，显然 那么  ，选C。点评：本题通过 产生构成方程组，再由方程组得到，进一步发现了周期函数，显然，构造方程是求解的关键。例4、已知函数 在R上满足 ，则曲线 在点 处的切线方程是 （A）  （B） （C） （D） 解析：由 得 ，即  ，消去 得 ∴ ，∴切线方程为 ，即 选A点评：本题中存在着一个明显的变量 ，只有将其消去，才能产生函数的解析式，于是，想到了通过替换产生另一个式子组成方程组，来达到目的。3.数形结合 一望而解 “数少形时缺直观，形少数时难入微”它准确的告诉我们：数形结合，相得益彰；利用数、式进行深入细致的分析；利用图形直观又可以看出数、式的内在关系； 例5 已知函数 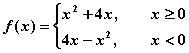 若 则实数 的取值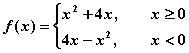范围是A  B  C  D   解析：作出 的图像，如右图由图像可知 在定义域内是增函数于是，由 得  故选择C。 点评：本题通过图形，立即发现函数是增函数，从而将函数值的不等关系转化为二次不等式，方便、快捷的产生了结论。 例6、若 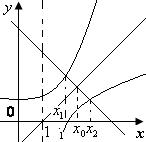 满足 ,  满足 , +＝（A） (B)3 (C)  (D)4 解析：由  ，令 则是两函数图像交点的横坐标。又由 ，再令  ，则两函数 图像交点的横坐标。由于  与的图像关于 对称，结合图像，易知  ，联立与 得  ，选C。点评：本题不仅要会画图，更重要的是善于分析图形的关系，当然，如果图形画的比较准确的话，凭直觉也许能提出较准确的猜想。 4.以静制动 稳中求胜 一个看似复杂的问题，细心观察之后，也许可以发现其中不变的东西，此时，我们可以建立在这些“不变”的基础上，以静制动。 例7 若存在过点  的直线与曲线 和 都相切，则等于 A．  或 B．或 C． 或 D．或 解析：设过  的直线与相切于点 ，所以切线方程为 ，即 ，又在切线上，则 或 ，当 时，由 与 相切可得 ，当 时，由 与相切可得 ，所以选 .点评：粗看此题似有难度，两个曲线存在公共切线，其中一个曲线还是未知的。其实，留心看一下，便会发现 过的切线方程是可以求出来的，它是不变的，于是建立在此直线的基础上促使问题获解。例8 设函数  ，曲线 在点 处的切线方程为 ，则曲线在点处切线的斜率为A．  B． C． D． 解析：由已知  ，而 ，所以 故选A。点评：本题中不变的量是  ，熟悉导数几何意义的考生一眼就看出了，抓它再看条件，很快便有了结论。5.揭示特征 速解图形 特征，是一事物区别于它事物的本质，抓住特征，就等于抓住了本质。面对图形问题，我们要认真观察、仔细分析，也许一、两个特征就是“破”题的关键。 例9 设 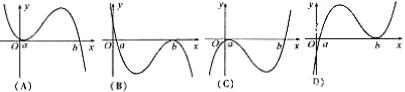＜b,函数 的图像可能是  解析：看看函数式，可以发现  时， ，再看图形特征，立即排除A、B；再看 时， ，再看图形，排除D，于是选C。点评：本题将函数特征与图形特征对照分析，很快排除了干扰支，产生正确结论。 例10 函数 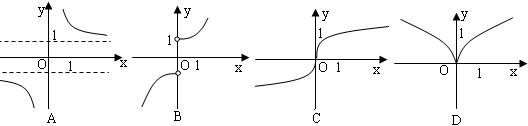 的图像大致为( ).  点评：首先由函数的定义域可得  ，看看图形，立即排除C、D。再由 即函数递减，选A。点评：上述两题若是想先作出图形，再对照选项选出结论的话，可能永远无法达到目的，揭示特征，为我们求解此类问题开辟新的通道。 6.灵活替换 攻防自如 替换，是一种策略，它可以变生疏为熟悉、变复杂为简单、变抽象为具体；当我们面对抽象、复杂问题时，若能灵活替换，可以说：攻防自如。 例11 函数 的定义域为R，若 与 都是奇函数，则( ) (A) 是偶函数 (B) 是奇函数 (C)  (D)  是奇函数解析：  与都是奇函数，得  由   即 是奇函数。故选D点评：本题的替换次数很多、也相当灵活，若有一步不慎，可能产生不了结论，或是产生错误结论。 例12 已知定义在R上的奇函数 ，满足 ,且在区间[0,2]上是增函数,则( ). A.  B.  C.  D.  解析：因为 满足 ，所以函数是以8为周期的周期函数, 则 , , ,又因为在R上是奇函数，  ,得 , ,而由得 ,又因为在区间[0,2]上是增函数,所以 ,所以 ,即,故选D. 点评：本题有两类替换，其一是函数式的替换，通过这种替换让我们看到了周期函数。其二是函数值的替换，这方面主要利用周期函数与奇函数，两者缺一不可。 7.最值转化 直击命脉 最值是函数的重要特征量，很多命题人总是喜欢在此处作文章。请看： 例13 设函数 在（ ，+ ）内有定义。对于给定的正数K，定义函数 取函数 。若对任意的 ，恒有 =，则 A．K的最大值为2 B. K的最小值为2 C．K的最大值为1 D. K的最小值为1 解析：由  知 ，所以 时， ，当 时， ，所以 即的值域是 ，而要使 在上恒成立，则必有 ，于是 。故选D项。点评：本题中“恒有 =”其实就是“”恒成立，于是只需求出的最大值即可。例14 把函数  的图像 向右平移 个单位长度，再向下平移 个单位长度后得到图像 ．若对任意的 ，曲线与至多只有一个交点，则的最小值为（ ）A． B． C． D． 解析：设曲线 的解析式为 则方程  ，即 ，即 对任意恒成立，于是的最大值，令 则 由此知函数 在（0，2）上为增函数，在 上为减函数，所以当 时，函数取最大值，即为4，于是 。点评：本题将图像平移与函数最值结合进行设计，可谓别出心裁。求解时，若能抓住最值，通过最值进行转化，也许一切都变得顺利。 8.抓住本质 应对创新 “万变不离其宗”，不论如何创新，本质的东西是改不了的。近年试题的创新力度大、新题层出不穷，当我们遇到创新问题时，一定要注意抓住本质，以本质为切入点，也许创新题就不是那么难了。 例15 对于正实数  ，记 为满足下述条件的函数构成的集合： 且 ，有 ．下列结论中正确的是 ( )A．若  ， ，则 B．若 ，，且 ，则 C．若 ，，则 21世纪教育网 D．若 ，，且 ，则 解析：对于 ，即有 ，令 ，有 ，不妨设，，即有  ，得 ，即．点评：本题的本质实际上是不等式的性质中“同向不等式相加”，其它选项分别为“同向不等式相减”、“同向不等式相除”、“同向不等式相乘”。抓住了它，很快产生结论。 例16 设函数  的定义域为 ，若所有点 构成一个正方形区域，则的值为A．  B． C． D．不能确定21世纪教育网 解析：由  ， ， ， ，选B点评：本题的实际上是定义域对应的区间长度与值域对应的区间长度相等。认识到此，求解也就变得易如反掌。 函数，中学数学的重要内容。在这片“广阔天地”中诞生了无数道好题，它让无数高考先辈们兴奋，也让无数高考先辈们无奈，你呢？有了这八招，也许会多一点兴奋。 (责任编辑：admin) |