|
利用定积分证明数列和型不等式 湖北省阳新县高级中学 邹生书 我们把形如  ( 为常数)或 的不等式称之为数列和型不等式，这类不等式常见于高中数学竞赛和高考压轴题中，由于证明难度较大往往令人望而生畏.其中有些不等式若利用定积分的几何意证明，则可达到以简驭繁、以形助数的解题效果.下面举例说明供参考.一、 (为常数)型例1(2007年全国高中数学联赛江苏赛区第二试第二题)已知正整数  ，求证 .分析 这是一边为常数另一边与自然数有关的不等式，标准答案是用数学归纳法证明比这个不等式更强的不等式  ，这个不等式是怎么来的令人费解.若由所证式子联想到在用定积分求曲边梯形面积的过程中“分割求和”这一步，则可考虑用定积分的几何意义求解.证明 构造函数  并作图象如图1所示.因函数在 上是凹函数，由函数图象可知，在区间 上的 个矩形的面积之和小于曲边梯形的面积， 图1 即  ，因为  ，所以 .所以 .例2 求证  .证明 构造函数  ，又 ，而函数  在上是凹函数，由图象知，在区间 上的 个矩形的面积之和小于曲边梯形的面积， 图2 即  ，所以  .例3 证明  。证明 构造函数  ，因 ，又其函数是凹函数，由图3可知，在区间 上 个矩形的面积之和小于曲边梯形的面积， 图3 即   .所以  .二、 型例4 若  ，求证: .证明 不等式链的左边是通项为 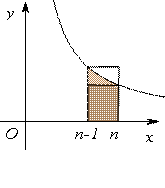 的数列的前项之和，右边通项为 的数列的前项之和，中间的 可当作是某数列的前项之和.故只要证当 时这三个数列的通项不等式 成立即可.构造函数 ，因为 ，作的图象，由图4知，在区间 上曲边梯形的面积大小在以区间长度1为一边长，以左右端点对应的函数值为另一边长的两个矩形面积之间，即 ，而 ，故不等式 成立，从而所证不等式成立. 图4 例5（2010年高考湖北卷理科第21题）已知函数  的图象在点 处的切线方程为 .（Ⅰ）用  表示出 ；（Ⅱ）若  在 内恒成立，求的取值范围；（Ⅲ）证明:  .本题第三问不等式的证明是本大题也是本卷的压轴戏，具有综合性强、难度大、思维含金量高、区分度大等特点.这个不等式的证明既可用第二问的结论证明也可用定积分来证明. 证明 （Ⅲ）不等式 左边是通项为的数列的前项之和，我们也可把右边当作是通项为 的数列的前项之和 ，则当时， ，此式适合 ，故只要证当 时， 即 ，也就是要证  .由此构造函数 ，并作其图象如图5所示.由图知，直角梯形的面积大于曲边梯形的面积，即 . 图5 而  ，所以，故原不等式成立. 点评 本解法另辟蹊径，挖掘新的待证不等式左右两边的几何意义，通过构造函数利用定积分的几何意义来解决问题，解法虽然综合性强，但由于数形结合解法直观便于操作.积分法是在新课标下证明不等式的一个新方法新亮点，很值得品味.由例4例5可知，要解决这类复杂问题的关键是要善于联想善于分析问题和转化问题，这样才能化繁为简、化难为易，精彩的解法不是空穴来风而是理性思维的必然结果. 作者简介：邹生书，男，1962年12月出生，湖北阳新县人.现任教于阳新县高级中学，中学数学高级教师，黄石市骨干教师.近四年来在《数学通讯》、《数学通报》、《中学数学教学参考》、《中学数学教学》、《中学数学月刊》、《中学数学》、《中学教研》、《中学数学研究》、《中小学数学》、《高中数学教与学》、《中学生数学》、《河北理科教学研究》、《数理天地》、《数理化解题研究》等近二十种期刊上发表教学教研文章百余篇，在人教网中学数学栏目发表文章二十多篇. (责任编辑：admin) |