|
五彩缤纷的数列归纳推理题 湖北省阳新县高级中学 邹生书 归纳推理题以能力立意，重点考查学生的直觉思维能力，考查观察、分析、猜想和归纳能力，归纳推理题已成为新课标数学高考的热点考题。纵览高考题和模拟题，数列归纳推理题其表现形式真可谓是五彩缤纷千姿百态，本文按表现形式分类解析数列归纳推理题的解法，供大家参考。 1.表格类 例 1 （2010年高考浙江卷）在如下数表中，已知每行每列中的数都成等差数列，
那么位于表中的第  行第 列的数是 。解法1 考察第 行从左至右所构成的数列 。依数表的规律知是首项为公差为的等差数列，所以 。解法2 考察表中第 行第列的数所构成的数列 。依题意得 ， ，由数表规律知 ，将上述各项换一种呈现方式得， ，由此不难归纳出 。评注 解决本题的关键是将所求的数放在一个数列中进行考察，只要求出该数列的通项公式则问题迎刃而解。解法1是考察第 行从左至右所构成的数列，解法2考察表中第行第个数所构成的数列，尽管解题切入点和视角不同但所得结果同。2.图案类 例2某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的中个图案都是由小正方形构成，小正方形数越多刺绣越漂亮。现按同样的规刺绣（小正方形的摆放规律相同），设第 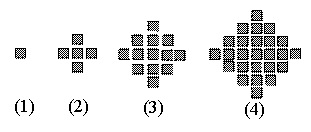个图形包含 个小正方形，则的表达式为＿＿＿ 解 观察得   ，故应填 。例3 一同学在电脑中打出了如下若干个圈：○●○○●○○○●○○○○●○○○○○●…若此若干个圈依此规律继续下去，得到一系列的圈，那么在前120个圈中的●个数是（ ）    D.15解 题目中圆圈是一字长蛇阵排列，构造数列  ，其中 表示第个黑圈及前面所有圆圈的个数。观察排列规律易得， ，或 。令 ，解得 ，故应选 。3.渐开线格点类 例4（2010年福建信息卷）将平面直角坐标系中的格点（横、纵坐标均为整数的点）按如下规则标上数字标签：原点处标 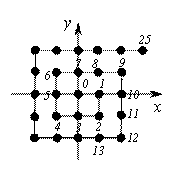 ，点 处标 ，点 处标 ，点 处标 ，点 处标 ，点 处标 ，依此类推，则标签 的格点的坐标为＿＿。 解析 华罗庚教授曾指出：“善于退'，足够地'退'，退到最原始而不失重要性的地方，退到我们容易看清问题的地方，是学好数学的一个诀窍.”，“以退求进”策略是归纳推理的基本策略。因为 为奇数的平方，所以我们只需考察奇数的平方。因为标签为 所对应的点为；标签为 所对应的点为 ；依题意点的渐开规律知标签为 所对应的点为 ； ，于是猜想：标签为 所对应的点为 。令 得 ，所以标签为的格点的坐标为 。 评注 本解法的关键是从要复杂的问题情景中通过观察、分析、比较和猜想，最终将问题转化为考察奇数的平方所成的数列与对应的点的坐标间的关系。 4.左右摆动格点类 例5 如图，坐标纸上的每个单元格的边长为1，由下往上的 6个点：  的横纵坐标对应数列 的前12项,  ，则 ( )     解 将数列 按脚标被4除所得的余数分类列表如下，由表发现  ， ， ，…，依此规律得 ，故选 。点评 改变一下呈现方式，规律很可能就会变得清晰可见。当你一筹莫展无计可施时，不妨改变一下问题的表现形式，也许问题会变得豁然开朗奇迹就在不经意间出现。 5.等腰直角三角形数阵 例6 把正整数按一定规则排成如图所示的三角形数表。设  是位于这个三角形数表中从上往下数第 行，从左往右数第 个数，如 。若 ，则与的和为＿＿＿解析 观察三角形数表知，第 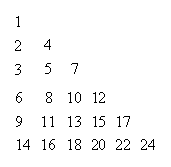行有个数，且奇数行均为奇数，偶数行均为偶数，从第二行开始自左至右构成公差为2的等差数列。因为 为奇数，所以它在奇数行，故只需考察奇数行第一个数所构成的数列特征即可。根据三角形数表的排列规则，奇数行第一个数所构成的数列为 ， 。 用差分法得：  ，由此发现：数列  是首项为2，公差为4项数为 的等差数列，其前 项的和为 ，所以 。假设在第 行上，则 ，解得 ，所以 ，即在第63行上。于是第63行的第一个数是 ，所以第63行自左至右构成首项为 公差为2的等差数列，设是该数列的第项，则有 ，解得 。故是三角形数表中的第63行自左至右第45个数，故 。评注 本题问题情景错综复杂，从解法知本题需要考察两个数列，其中奇数行第一个数所构成的数列通项公式的获得，是问题解决的关键有一定难度，此外通过解不等式确定所求的数所在的行数又是一个难点，本题综合能力要求较高是一道难题。 6.倒立等边三角形数阵 例7 给定倒三角形数表如图①所示，其中第一行各数依次是  ，从第二行起每一个数分别等于上一行左右两数之和，最后一行只有一个数M，则这个数M是＿＿。1 2 3 … 2007 2008 2009 1 2 3 4 5 6 7 3 5 … 4015 4017 3 5 7 9 11 13 8 … 8032 8 12 16 20 24 … 20 28 36 44 48 64 80  112 144M 256 图① 图② 解析 由数表构成规律知，这个数表共有  行为奇数行， 是最后一个数字。以退为进，采用归纳法。考察行数为奇数的倒三角形数表的最后一个数字所构成的数列 ，由图②知， 。将其换成如下呈现方式： ，据此不难归纳出 。令得，所以 。评注 笔者在文[1]中给出了三种解题思路分析和相应的解法，上述解法相对文[1]的三种解法而言要显得简单些。由此可见，数列的选择直接影响问题解决的难易，根据具体问题选择一个适当的数列进行考察也是解题的一个关键。 7.等腰梯形数阵 例8（湖南07年高考题）将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的  三角数表。从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，，第次全行的数都为1的是第＿＿行；第61行中1的个数是＿＿。解析（1）依题意，通过列举、观察发现全行都是1的行数所构成的数列 为 ，归纳知 ，故第次全行的数都为1的是第 行。 （2）由（1）知第63行全为1，依题意逆推而上知第62行的63个数分别为  ，其规律是 为一个周期，周期为2，共有31个周期最后一项为1；逆推而上，第61行的62个数分别为 ，其规律是 为一个周期，周期为4，共有15个周期，最后两项为 ，所以第61行中1的个数是 。评注 此题是由课本中的“杨辉三角”进行“再创造”而来，背景熟悉似曾相识却不落俗套富有创意。着重考查学生的观察、归纳、猜想能力以及综合分析问题和解决问题的能力，思维层次要求较高。 8.分解式型 例9（2011湖北百所重点中学五月高三联考理科第14题）对于大于或等于2的自然数  的 次幂有如下分解方式： ； ，根据上这分解规律，若  ，则 ＿＿；若 的分解式中含有数 ，则 ＿＿。解 易求得  ；本题的重头戏是求 。观察发现： 的分解式是个连续奇数之和。考察 分解式中第一个数所构成的数列： 。法1 用差分法得，  ，由此发现：数列 是首项为4，公差为2项数为 的等差数列，则其前项的和为 ，所以 。因为的分解式中含有数，所以 ，解得 ，由此知 。法2 将分解式中第一个数所构成的数列 换成如下呈现方式（注：这并不是法1结果地直接运用）： ， ，由此发现，下同法1略。9.新定义型 例10（2011年高考湖南卷理科第15题）若数列 满足：对任意的 ，只有有限个正整数使得 成立，记这样的的个数为 ，则得到一个新数列 。例如，若列是 ，则数列是 。已知对任意的， ，则 ＿＿， ＿＿。解析 由  得 ，又 ，所以 ，所以 。由 得 ，令 同上可求得。实际上就是满中不等式的正整数解的个数。可求得数列的各项依次为： ，由此得 ， ， ，由此猜想： 。评注 本题以数列为背景，通过新定义考查学生的自学能力、创新能力和探究能力。解题的关键是理解新定义的含义并将抽象的定义转化具体的数列。 10.隐性寄生型 例11（2011年高考福建卷文科第15题）观察下列等式： ①  ；②  ；③  ；④  ；⑤  。可以推测  ＿＿。解析（1）先求 。观察每个等式最高次幂的系数所构成的数列，因为 ， ，不难发现这是一个公比为4的等比数列，所以 。（2）求  。观察每个等式中 的系数所构成的数列 ： ， 。如果我们将数列换一种表现形式，奇迹就会在变中出现，其内隐的规律性也就昭然若揭了。下面我们来看几种有效的呈现方式：方式1：  ，由此得  。方式2：  ，由此得 。方式3：  ，据此得 。（3）求 。法1（赋值法）：在⑤式中令  得， ，解得 。法2（观察法）：观察前4个等式右边知各项系数和均为1，由此猜想⑤式右边知各项系数和也为1，从而求得 。综上可知  。评注 本题以三角公式为背景，重点考查观察、分析、猜想和归纳推理的能力，考查归纳法和赋值法等重要数学思想方法。本题求 是一个难点，关键是将所考察的数列进行形式上的变化，使其内隐的规律化隐为显。参考文献： 邹生书。解一个三角形数表题的思维历程。数学通讯，2010（1-2）上半月。 (责任编辑：admin) |