|
线性规划解法赏析 内蒙古赤峰市翁牛特旗乌丹一中 熊明军 “最优化”问题中的简单线性规划是高考常考知识点，属于不等式模块，重点考查学生的动手操作能力。随着新课程改革的全面施行，现有的人教版教材把不等式内容进行了很大程度的推广和深化。高中数学的教学，不是把已有的简单问题复杂化，而是应该在比学生理解掌握的知识水平更低的层次来思考解决问题的方法，让学生感觉数学不是高不可攀的。因此，有必要对线性规划问题的解法做一下梳理强化，结合例题多策略求解，以便学生参考选择适合自己的方法。 （人教B版  ）例3  两个居民小区的居委会组织本小区的中学生，利用双休日去市郊的敬老院参加献爱心活动，两个小区都有同学参加。已知 小区的每位同学往返车费是3元，每人可为5位老人服务； 小区的每位同学往返车费是5元，每人可为3位老人服务。如果要求区参与活动的同学比区参与活动的同学多，且去敬老院的往返总车费不超过37元。怎样安排两区参与活动同学的人数，才能使受到服务的老人最多？受到服务的老人最多是多少？解：依题意可列表如下：
设 两区参与活动的人数分别为 、 ，则受到服务的老人的人数为 其中  满足下列条件 于是问题转化为，在 满足上述约束条件下，求式子的最大值。【解法一】线定界，点定域，距离确定最优解 ①在同一坐标系下作约束条件不等式对应的直线：不等式  、 与 对应的直线方程分别为 、 与 ；在同一平面直角坐标系中作出直线（实线）、（实线）与（实线）。②取特殊点确定约束条件表示的可行域：平面直角坐标系中的直线分为过原点和不过原点两类，不过原点的直线定域取特殊点 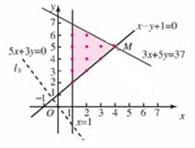 ；过原点的直线定域取特殊点 或 。 ③可行域中的点到目标函数直线  的距离确定最优解：作出直线 ： ，结合图中所示可行域，容易看出点 到直线的距离最大，若是整点，则是最优解。【解法二】线定界，号定域，距离确定最优解 ①在同一坐标系下作约束条件不等式对应的直线。（同解法一） ②将约束条件中各不等式的 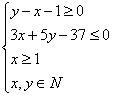项系数变为正数： 。由下列结论，通过不等号来确定约束条件表示的可行域： （或 ），且 ，则不等式所表示的平面区域为直线上方（大于 上）； （或 ），且，则不等式所表示的平面区域为直线下方（小于下）。③可行域中的点到目标函数直线 的距离确定最优解：作出直线：，结合图中所示可行域，容易看出点到直线的距离最大，若是整点，则是最优解。【解法三】线定界，方向定域，距离确定最优解 ①在同一坐标系下作约束条件不等式对应的直线。（同解法一） ②约束条件化为：  ，直线 （不同时为0）的一个法向量为 （设其以坐标原点为始点），由下列结论确定约束条件表示的可行域：（或），则不等式所表示的平面区域为 同向（大于同向）；（或），则不等式所表示的平面区域为反向（小于反向）。③可行域中的点到目标函数直线 的距离确定最优解：作出直线：，结合图中所示可行域，容易看出点到直线的距离最大，若是整点，则是最优解。(责任编辑：admin) |
