|
共线向量的三个命题及应用 广东省中山一中高中部 许少华 命题1:若两非零向量 命题2:若两向量 命题3:若向量 命题1、2的正确性是显然的,对于命题3可用反证法,再借助于命题2很快予以证明,本文例说上述三命题在解题中的应用 1.证三点共线 例1 已知两非零向量 证明:由 得向量 故 点评:欲证 2.证几何题 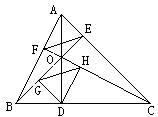 例2 已知 证明: 又 即 因此, 点评:将平几问题转化为向量问题,欲证 3.求向量 例3 在 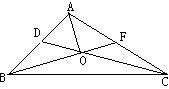 解:由于 又 由于 即 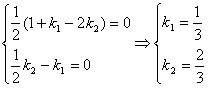 点评:用已知向量表示未知向量,往往有一定的难度。面对图形中错综复杂的线条,要善于抓关键、抓重点,有时还要借助于参数;本题借助于参数且两次利用三点共线,再结合向量的线性表示结论; 4.解探索性题 例4 若 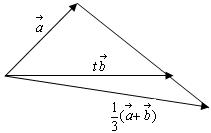 解:若存在,则必存在实数 由于 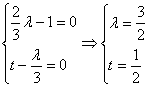 故存在实数 点评:先假设结论存在,然后进行推理,出现矛盾,说明不存在,否则结论存在是求解探索性问题的常规思路;本题先假定三终点共线,产生“ (责任编辑:admin) |
