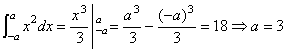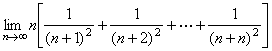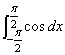错解剖析得真知(三十二)
§10.2导数的应用
一、 知识导学
1.可导函数的极值
(1)极值的概念
设函数 在点 在点 附近有定义,且若对 附近有定义,且若对 附近的所有的点都有 附近的所有的点都有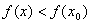 (或 (或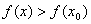 ),则称 ),则称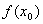 为函数的一个极大(小)值,称 为函数的一个极大(小)值,称 为极大(小)值点. 为极大(小)值点.
(2)求可导函数 极值的步骤: 极值的步骤:
①求导数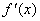 。求方程 。求方程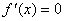 的根. 的根.
②求方程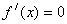 的根. 的根.
③检验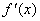 在方程 在方程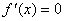 的根的左右的符号,如果在根的左侧附近为正,右侧附近为负,那么函数 的根的左右的符号,如果在根的左侧附近为正,右侧附近为负,那么函数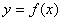 在这个根处取得极大值;如果在根的右侧附近为正,左侧附近为负,那么函数 在这个根处取得极大值;如果在根的右侧附近为正,左侧附近为负,那么函数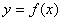 在这个根处取得极小值. 在这个根处取得极小值.
2.函数的最大值和最小值
(1)设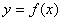 是定义在区间 是定义在区间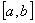 上的函数, 上的函数,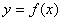 在 在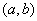 内有导数,求函数 内有导数,求函数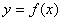 在 在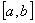 上的最大值与最小值,可分两步进行. 上的最大值与最小值,可分两步进行.
①求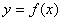 在 在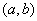 内的极值. 内的极值.
②将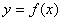 在各极值点的极值与 在各极值点的极值与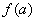 、 、 比较,其中最大的一个为最大值,最小的一个为最小值. 比较,其中最大的一个为最大值,最小的一个为最小值.
(2)若函数 在 在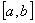 上单调增加,则 上单调增加,则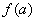 为函数的最小值, 为函数的最小值, 为函数的最大值;若函数 为函数的最大值;若函数 在 在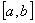 上单调递减,则 上单调递减,则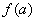 为函数的最大值, 为函数的最大值, 为函数的最小值. 为函数的最小值.
二、疑难知识导析
1.在求可导函数的极值时,应注意:(以下将导函数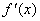 取值为0的点称为函数 取值为0的点称为函数 的驻点可导函数的极值点一定是它的驻点,注意一定要是可导函数。例如函数 的驻点可导函数的极值点一定是它的驻点,注意一定要是可导函数。例如函数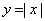 在点 在点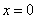 处有极小值 处有极小值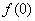 =0,可是这里的 =0,可是这里的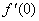 根本不存在,所以点 根本不存在,所以点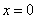 不是 不是 的驻点. 的驻点.
(1) 可导函数的驻点可能是它的极值点,也可能不是极值点。例如函数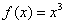 的导数 的导数 ,在点 ,在点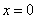 处有 处有 ,即点 ,即点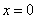 是 是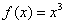 的驻点,但从 的驻点,但从 在 在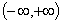 上为增函数可知,点 上为增函数可知,点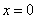 不是 不是 的极值点. 的极值点.
(2) 求一个可导函数的极值时,常常把驻点附近的函数值的讨论情况列成表格,这样可使函数在各单调区间的增减情况一目了然.
(3) 在求实际问题中的最大值和最小值时,一般是先找出自变量、因变量,建立函数关系式,并确定其定义域.如果定义域是一个开区间,函数在定义域内可导(其实只要是初等函数,它在自己的定义域内必然可导),并且按常理分析,此函数在这一开区间内应该有最大(小)值(如果定义域是闭区间,那么只要函数在此闭区间上连续,它就一定有最大(小).记住这个定理很有好处),然后通过对函数求导,发现定义域内只有一个驻点,那么立即可以断定在这个驻点处的函数值就是最大(小)值。知道这一点是非常重要的,因为它在应用上较为简便,省去了讨论驻点是否为极值点,求函数在端点处的值,以及同函数在极值点处的值进行比较等步骤.
2.极大(小)值与最大(小)值的区别与联系
极值是局部性概念,最大(小)值可以看作整体性概念,因而在一般情况下,两者是有区别的.极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值,但如果连续函数在区间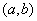 内只有一个极值,那么极大值就是最大值,极小值就是最小值. 内只有一个极值,那么极大值就是最大值,极小值就是最小值.
三、经典例题导讲
[例1]已知曲线 及点 及点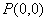 ,求过点 ,求过点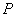 的曲线 的曲线 的切线方程. 的切线方程.
错解: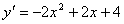 , , 过点 过点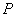 的切线斜率 的切线斜率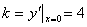 , , 过点 过点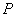 的曲线 的曲线 的切线方程为 的切线方程为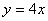 . .
错因:曲线在某点处的切线斜率是该曲线对应的函数在该点处的导数值,这是导数的几何意义.在此题中,点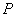 凑巧在曲线 凑巧在曲线 上,求过点 上,求过点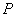 的切线方程,却并非说切点就是点 的切线方程,却并非说切点就是点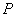 ,上述解法对求过点 ,上述解法对求过点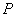 的切线方程和求曲线在点 的切线方程和求曲线在点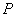 处的切线方程,认识不到位,发生了混淆. 处的切线方程,认识不到位,发生了混淆.
正解:设过点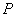 的切线与曲线 的切线与曲线 切于点 切于点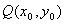 ,则过点 ,则过点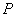 的曲线 的曲线 的切线斜率 的切线斜率
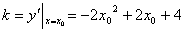 ,又 ,又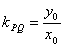 , , 。① 。① 点 点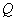 在曲线 在曲线 上, 上,
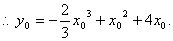 ②,②代入①得 ②,②代入①得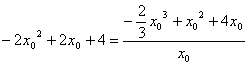
化简,得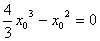 , , 或 或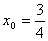 .若 .若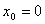 ,则 ,则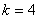 ,过点 ,过点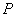 的切线方程为 的切线方程为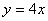 ;若 ;若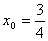 ,则 ,则 ,过点 ,过点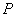 的切线方程为 的切线方程为  过点 过点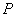 的曲线 的曲线 的切线方程为 的切线方程为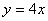 或 或
[例2]已知函数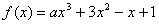 在 在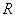 上是减函数,求 上是减函数,求 的取值范围. 的取值范围.
错解:   在 在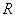 上是减函数, 上是减函数, 在 在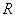 上恒成立, 上恒成立,
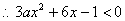 对一切 对一切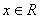 恒成立, 恒成立, ,即 ,即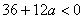 , ,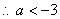 . .
正解: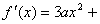 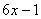 , ,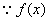 在 在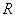 上是减函数, 上是减函数, 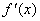  在 在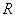 上恒成立, 上恒成立,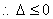 且 且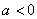 ,即 ,即 且 且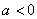 , ,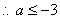 . .
[例3]当  ,证明不等式 ,证明不等式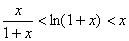 . .
证明: , ,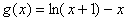 ,则 ,则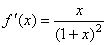 ,当 ,当 时。 时。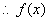 在 在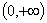 内是增函数, 内是增函数,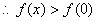 ,即 ,即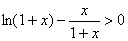 ,又 ,又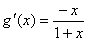 ,当 ,当 时, 时,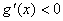 , ,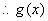 在 在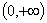 内是减函数, 内是减函数,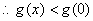 ,即 ,即 ,因此,当 ,因此,当 时,不等式 时,不等式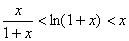 成立. 成立.
点评:由题意构造出两个函数 , ,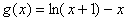 .利用导数求函数的单调区间,从而导出 .利用导数求函数的单调区间,从而导出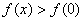 及 及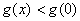 是解决本题的关键. 是解决本题的关键.
[例4]设工厂到铁路线的垂直距离为20km,垂足为B.铁路线上距离B为100km处有一原料供应站C,现要在铁路BC之间某处D修建一个原料中转车站,再由车站D向工厂修一条公路.如果已知每千米的铁路运费与公路运费之比为3:5,那么,D应选在何处,才能使原料供应站C运货到工厂A所需运费最省?
解 : 设BD之间的距离为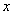 km,则|AD|= km,则|AD|=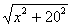 ,|CD|= ,|CD|=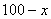 .如果公路运费为 .如果公路运费为 元/km,那么铁路运费为 元/km,那么铁路运费为 元/km.故从原料供应站C途经中转站D到工厂A所需总运费 元/km.故从原料供应站C途经中转站D到工厂A所需总运费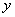 为: 为: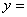 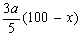 + + 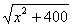 ,( ,(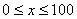 ).对该式求导,得 ).对该式求导,得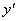 = =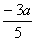 + +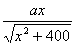 = =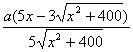 ,令 ,令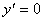 ,即得25 ,即得25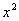 =9( =9(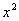 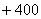 ),解之得 ),解之得
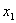 =15, =15,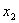 =-15(不符合实际意义,舍去).且 =-15(不符合实际意义,舍去).且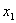 =15是函数 =15是函数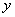 在定义域内的唯一驻点,所以 在定义域内的唯一驻点,所以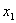 =15是函数 =15是函数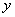 的极小值点,而且也是函数 的极小值点,而且也是函数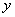 的最小值点.由此可知,车站D建于B,C之间并且与B相距15km处时,运费最省. 的最小值点.由此可知,车站D建于B,C之间并且与B相距15km处时,运费最省.
点评: 这是一道实际生活中的优化问题,建立的目标函数是一个复合函数,用过去的知识求其最值往往没有一般方法,即使能求出,也要涉及到较高的技能技巧.而运用导数知识,求复合函数的最值就变得非常简单.一般情况下,对于实际生活中的优化问题,如果其目标函数为高次多项式函数、简单的分式函数简单的无理函数、简单的指数、对数函数,或它们的复合函数,均可用导数法求其最值.由此也可见,导数的引入,大大拓宽了中学数学知识在实际优化问题中的应用空间.
[例5](2006年四川)函数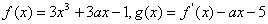 ,其中 ,其中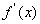 是 是 的导函数.(1)对满足-1≤ 的导函数.(1)对满足-1≤ ≤1的一切 ≤1的一切 的值,都有 的值,都有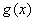 <0,求实数 <0,求实数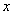 的取值范围; 的取值范围;
(2)设 =- =- ,当实数 ,当实数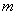 在什么范围内变化时,函数 在什么范围内变化时,函数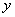 = = 的图象与直线 的图象与直线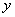 =3只有一个公共点. =3只有一个公共点.
解:(1)由题意
令 , ,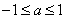
对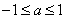 ,恒有 ,恒有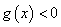 ,即 ,即
∴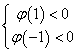 即 即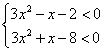
解得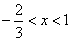
故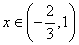 时,对满足-1≤ 时,对满足-1≤ ≤1的一切 ≤1的一切 的值,都有 的值,都有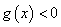 . .
(2)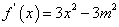
①当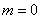 时, 时, 的图象与直线 的图象与直线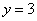 只有一个公共点 只有一个公共点
②当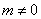 时,列表: 时,列表:
∴
又∵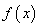 的值域是 的值域是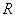 ,且在 ,且在 上单调递增 上单调递增
∴当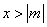 时函数 时函数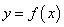 的图象与直线 的图象与直线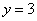 只有一个公共点. 只有一个公共点.
当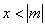 时,恒有 时,恒有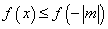
由题意得
即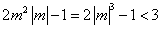
解得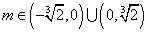
综上,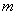 的取值范围是 的取值范围是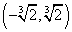 . .
[例6]若电灯B可在桌面上一点O的垂线上移动,桌面上有与点O距离为 的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?( 的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(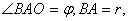 照度与 照度与 成正比,与 成正比,与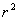 成反比) 成反比)
分析:如图,由光学知识,照度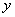 与 与 成正比,与 成正比,与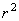 成反比,即 成反比,即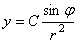 ( (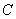 是与灯光强度有关的常数)要想点 是与灯光强度有关的常数)要想点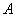 处有最大的照度,只需求 处有最大的照度,只需求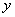 的极值就可以了. 的极值就可以了.
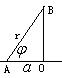
解:设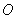 到 到 的距离为 的距离为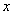 ,则 ,则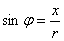 , ,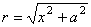
于是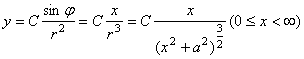 , ,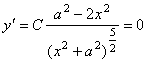 . .
当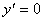 时,即方程 时,即方程 的根为 的根为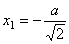 (舍)与 (舍)与 ,在我们讨论的半闭区间 ,在我们讨论的半闭区间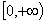 内,所以函数 内,所以函数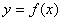 在点 在点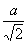 取极大值,也是最大值。即当电灯与 取极大值,也是最大值。即当电灯与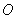 点距离为 点距离为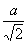 时,点 时,点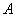 的照度 的照度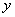 为最大. 为最大.
点评:在有关极值应用的问题中,绝大多数在所讨论的区间上函数只有一点使得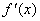 =0且在该点两侧, =0且在该点两侧,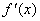 的符号各异,一般称为单峰问题,此时,该点就是极值点,也是最大(小)值点. 的符号各异,一般称为单峰问题,此时,该点就是极值点,也是最大(小)值点.
四、典型习题导练
1.已知函数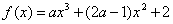 ,若 ,若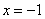 是 是 的一个极值点,则 的一个极值点,则 值为 ( ) 值为 ( )
A.2 B.-2 C.  D.4 D.4
2.已知函数 在 在 处有极值为10,则 处有极值为10,则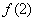 = . = .
3.给出下列三对函数:①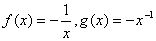 ② ②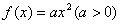 , ,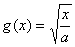
③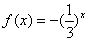 , ,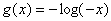 ;其中有且只有一对函数“既互为反函数,又同是各自定义域上的递增函数”,则这样的两个函数的导函数分别是 ;其中有且只有一对函数“既互为反函数,又同是各自定义域上的递增函数”,则这样的两个函数的导函数分别是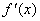 , , . .
4.已知函数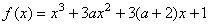 有极大值和极小值,求 有极大值和极小值,求 的取值范围. 的取值范围.
5.已知抛物线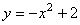 ,过其上一点 ,过其上一点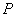 引抛物线的切线 引抛物线的切线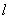 ,使 ,使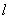 与两坐标轴在第一象限围成的三角形的面积最小,求 与两坐标轴在第一象限围成的三角形的面积最小,求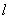 的方程. 的方程.
6.设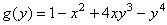 在 在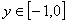 上的最大值为 上的最大值为 , ,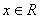 , ,
(1)求 的表达式;(2)求 的表达式;(2)求 的最大值. 的最大值.
§10.3定积分与微积分基本定理
一、知识导学
1.可微:若函数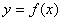 在 在 的增量 的增量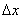 可以表示为 可以表示为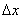 的线性函数 的线性函数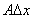 ( (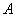 是常数)与较 是常数)与较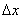 高阶的无穷小量之和: 高阶的无穷小量之和: (1),则称函数 (1),则称函数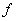 在点 在点 可微,(1)中的 可微,(1)中的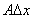 称为函数 称为函数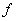 在点 在点 的微分,记作 的微分,记作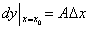 或 或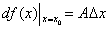 .函数 .函数 在点 在点 可微的充要条件是函数 可微的充要条件是函数 在 在 可导,这时(1)式中的 可导,这时(1)式中的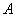 等于 等于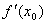 .若函数 .若函数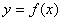 在区间 在区间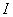 上每点都可微,则称 上每点都可微,则称 为 为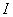 上的可微函数.函数 上的可微函数.函数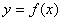 在 在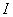 上的微分记作 上的微分记作 . .
2.微积分基本定理:如果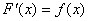 ,且 ,且 在 在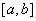 上可积.则 上可积.则
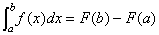 .其中 .其中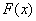 叫做 叫做 的一个原函数. 的一个原函数.
由于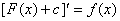 , ,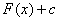 也是 也是 的原函数,其中 的原函数,其中 为常数. 为常数.
二、疑难知识导析
1 .定积分的定义过程包括“分割、近似求和、取极限”这几个步骤,这里包含着很重要的数学思想方法,只有对定积分的定义过程了解了,才能掌握定积分的应用.
1)一般情况下,对于区间的分割是任意的,只要求分割的小区间的长度的最大者 趋近于0,这样所有的小区间的长度才能都趋近于0,但有的时候为了解题的方便,我们选择将区间等份成 趋近于0,这样所有的小区间的长度才能都趋近于0,但有的时候为了解题的方便,我们选择将区间等份成 份,这样只要2其中的使 份,这样只要2其中的使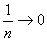 就可以了. 就可以了.
2)对每个小区间内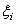 的选取也是任意的,在解题中也可选取区间的左端点或是右端点. 的选取也是任意的,在解题中也可选取区间的左端点或是右端点.
3)求极限的时候,不是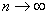 ,而是 ,而是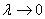 . .
2.在微积分基本定理中,原函数不是唯一的,但我们只要选取其中的一个就可以了,一般情况下选那个不带常数的。因为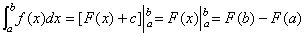 . .
3.利用定积分来求面积时,特别是位于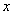 轴两侧的图形的面积的计算,分两部分进行计算,然后求两部分的代数和. 轴两侧的图形的面积的计算,分两部分进行计算,然后求两部分的代数和.
三 、经典例题导讲
[例1]求曲线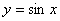 与 与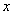 轴在区间 轴在区间 上所围成阴影部分的面积S. 上所围成阴影部分的面积S.
错解:分两部分,在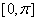 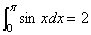 ,在 ,在 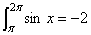 ,因此所求面积 ,因此所求面积 为 2+(-2)=0。 为 2+(-2)=0。
分析:面积应为各部分积分的代数和,也就是第二部分的积分不是阴影部分的面积,而是面积的相反数。所以不应该将两部分直接相加。
正解: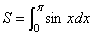 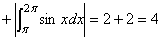
[例2]用微积分基本定理证明
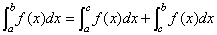 ( (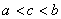 ) )
分析:即寻找 的原函数代入进行运算。 的原函数代入进行运算。
解;设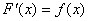 ,则 ,则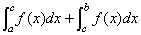
=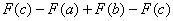 = =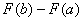
由微积分基本定理的逆运用可知:上式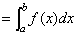
所以原式成立,即证。
注:该式可用来求分布在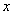 轴两侧的图形的积分。 轴两侧的图形的积分。
[例3]根据等式求常数 的值。 的值。
1)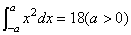 2) 2)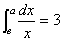
分析:利用微积分基本定理,求出原函数代入 求解 求解
解:1)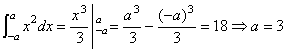
2)
[例4]某产品生产x个单位时的边际收入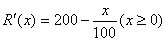
(1) 求生产了50个单位时的总收入。
(2) 如果已生产了100个单位时,求再生产100个单位时的总收入。
分析:总收入为边际收入的积分和,求总收入既为求边际收入在规定时间内的定积分。由收入函数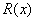 和边际收入 和边际收入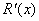 的关系可得 的关系可得
(1)生产50个单位时的总收入为
= =99875 =99875
(2)已生产了100个单位时后,再生产100个单位时的总收入为
答:生产50个单位时的总收入为99875;生产了100个单位时后,再生产100个单位时的总收入为19850.
[例5]一个带电量为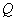 的电荷放在 的电荷放在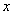 轴上原点处,形成电场,求单位正电荷在电场力作用下沿 轴上原点处,形成电场,求单位正电荷在电场力作用下沿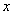 轴方向从 轴方向从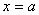 处移动到 处移动到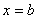 处时电场力对它所作的功。 处时电场力对它所作的功。
分析:变力做功的问题就是定积分问题在物理方面的应用。
解:单位正电荷放在电场中,距原点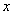 处,电荷对它的作用力为 处,电荷对它的作用力为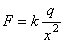
在单位电荷移动的过程中,电场对它的作用力为变力。则根据课本对变力做功的分析可知
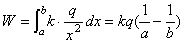
答:电场力对它做的功为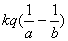 。 。
[例6]一质点以速度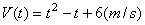 沿直线运动。求在时间间隔 沿直线运动。求在时间间隔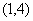 上的位移。 上的位移。
分析:变速求位移和变力求功一样都可以用定积分解决。
解: 
答:位移为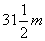 。 。
四、典型习题导练
1.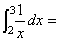 ( ) ( )
A.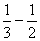 B. B.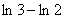 C. C.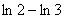 D. D.
2.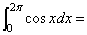 ( ) ( )
A.0 B.2 C.-2 D.4
3.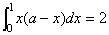 ,则 ,则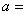 。 。
4.利用概念求极限: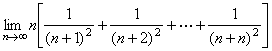
5.求下列定积分;
(1)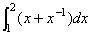 (2) (2)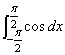
6.写出下面函数在给定区间上的总和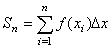 及 及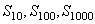 的表达式 的表达式
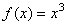 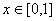
(责任编辑:admin) |
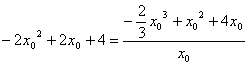
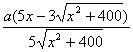 ,令
,令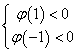 即
即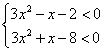

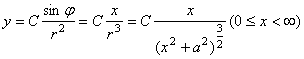 ,
,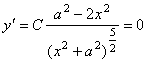 .
.