例说差分法在数列中的应用
湖北省阳新县高级中学 邹生书
自变量取值为正整数的函数 称为离散函数,称函数 称为离散函数,称函数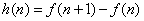 为函数 为函数 的一阶差分, 的一阶差分,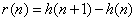 为函数 为函数 的二阶差分.等差数列 的二阶差分.等差数列 的通项 的通项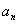 是前 是前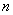 项和 项和 的一阶差分,公差是通项 的一阶差分,公差是通项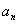 的一阶差分是前 的一阶差分是前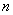 项和 项和 的二阶差分.差分是微分即导数的离散形式,导数是研究函数单调性和最值性的重要工具,有时需要多次求导用到一阶导数、二阶导数研究函数,同样差分是研究数列与前 的二阶差分.差分是微分即导数的离散形式,导数是研究函数单调性和最值性的重要工具,有时需要多次求导用到一阶导数、二阶导数研究函数,同样差分是研究数列与前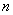 项和 项和 有关的问题的重要方法,有时需要多次作差要用到一阶差分二阶差分,本文举例说明差分法在解决与前 有关的问题的重要方法,有时需要多次作差要用到一阶差分二阶差分,本文举例说明差分法在解决与前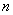 项和 项和 有关的数列证明、求数列通项和最值项等问题. 有关的数列证明、求数列通项和最值项等问题.
1.用差分法证明有关数列问题
例1 我们知道:若数列 是等差数列,则其前 是等差数列,则其前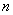 项和 项和 .反之,若数列 .反之,若数列 的前 的前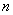 项和 项和 ,试判断数列 ,试判断数列 是否为等差数列?若是,请证明;若不是,请明理由. 是否为等差数列?若是,请证明;若不是,请明理由.
解 由 得 得 ①,由①得 ①,由①得 ②.②-①整理得, ②.②-①整理得, ③,由③得 ③,由③得 ④.④-③整理得, ④.④-③整理得, ,故数列 ,故数列 是等差数列. 是等差数列.
2.用差分法求数列通项
例2 数列 的前 的前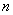 项和为 项和为 ,且 ,且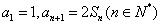 ,求数列 ,求数列 的通项 的通项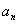 . .
分析 首先由差分法消去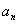 求出数列 求出数列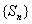 的通项公式,再由前 的通项公式,再由前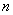 项和 项和 求出通项 求出通项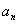 . .
解 因为当 时, 时,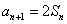 ,所以 ,所以 ,即 ,即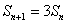 ,又 ,又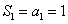 ,所以数列 ,所以数列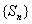 是首项为 是首项为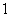 公比为 公比为 的等差数列,所以 的等差数列,所以 . .
当 时, 时, ,此式不适合 ,此式不适合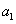 ,故数列 ,故数列 的通项 的通项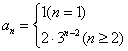 . .
例3 数列 满足 满足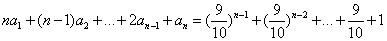
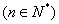 ,求数列 ,求数列 的通项公式. 的通项公式.
解 已知等式即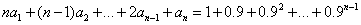 ①.由①得,当 ①.由①得,当 时, 时, ②. ②.
①-②得,当 时, 时, ③,此式适合 ③,此式适合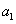 .由③得,当 .由③得,当 时, 时, ④.④-③得,当 ④.④-③得,当 时, 时,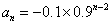 ,此式不适合 ,此式不适合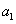 .故数列 .故数列 的通项公式为 的通项公式为 . .
例4(2010年高考江苏卷理科第19题)设各项均为正数的数列  的前 的前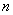 项和为 项和为 .已知 .已知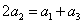 ,数列 ,数列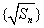 是公差为 是公差为 的等差数列.(Ⅰ)求数列 的等差数列.(Ⅰ)求数列 的通项公式(用 的通项公式(用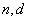 表示);(Ⅱ)略. 表示);(Ⅱ)略.
解(Ⅰ)依题意当 时, 时,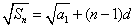 ,两边平方得, ,两边平方得,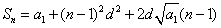 ①.于是当 ①.于是当 时,有 时,有 ②. ②.
①-②得,当 时, 时,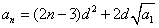 ③,此式表明当 ③,此式表明当 时数列 时数列 是等差数列.又 是等差数列.又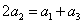 知 知 成等差数列,故当 成等差数列,故当 时数列 时数列 是等差数列.又当 是等差数列.又当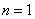 时,由③得, 时,由③得,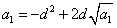 即 即 ,所以 ,所以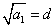 ,将其代入③得数列 ,将其代入③得数列 的通项公式为 的通项公式为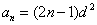 . .
评注1 题设中关于数列的前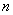 项和 项和 的恒等式是差分法的基础,利用 的恒等式是差分法的基础,利用 与通项 与通项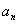 的关系 的关系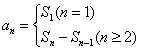 对关于 对关于 的恒等式通过一次作差或多次作差,直到能从所得关系中得出某个数列是等差数列或等比数列时差分法就算是完成任务;2、运用差分法时,要特别注意下标变量范围的变化与限制,用等差、等比数列定义时要指明该数列从第几项起是等差(比)数列,往往因起始项出错而使得分大打折扣. 的恒等式通过一次作差或多次作差,直到能从所得关系中得出某个数列是等差数列或等比数列时差分法就算是完成任务;2、运用差分法时,要特别注意下标变量范围的变化与限制,用等差、等比数列定义时要指明该数列从第几项起是等差(比)数列,往往因起始项出错而使得分大打折扣.
3.用差分法求数列最值项
例5 设数列 的前 的前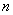 项和为 项和为 ,若对任意的 ,若对任意的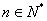 ,有 ,有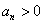 且 且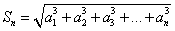 成立.(Ⅰ)求 成立.(Ⅰ)求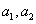 的值;(Ⅱ)求证:数列 的值;(Ⅱ)求证:数列 是等差数列,并写出其通项公式;(Ⅲ)令 是等差数列,并写出其通项公式;(Ⅲ)令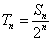 ,若对一切整数 ,若对一切整数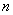 ,总有 ,总有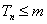 ,求 ,求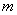 的取值范围. 的取值范围.
解(Ⅰ)求得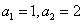 (过程略);(Ⅱ)(用差分法)由 (过程略);(Ⅱ)(用差分法)由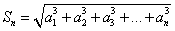 得, 得, ①.所以当 ①.所以当 时, 时, ②. ②.
①-②得,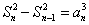 ,即 ,即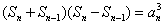 ,也就是 ,也就是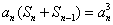 .又 .又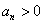 ,所以 ,所以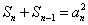 ③,于是当 ③,于是当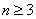 时,有 时,有 ④.③-④得, ④.③-④得,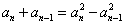 ,所以当 ,所以当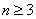 时, 时, .又 .又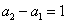 ,所以当 ,所以当 时, 时, ,所以数列 ,所以数列 是首项 是首项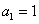 公差为1的等差数列,其通项为 公差为1的等差数列,其通项为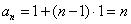 . .
(Ⅲ)由(Ⅱ)知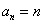 ,所以 ,所以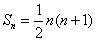 ,所以 ,所以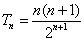 .因为对一切整数 .因为对一切整数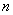 ,总有 ,总有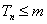 ,所以 ,所以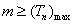 . .
因为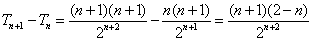 ,所以 ,所以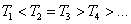 ,故 ,故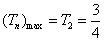 ,所以 ,所以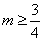 ,所以 ,所以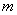 的取值范围是 的取值范围是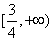 . .
例6 已知数列 满足 满足 , ,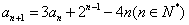 . .
(1)李四同学欲求 的通项公式,他想:如能找到一个函数 的通项公式,他想:如能找到一个函数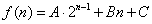 ( ( 是常数)把递推关系变成 是常数)把递推关系变成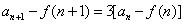 后,就容易求出 后,就容易求出 的通项公式了.请问:他设想的 的通项公式了.请问:他设想的 存在吗? 存在吗? 的通项公式是什么? 的通项公式是什么?
(2)记 ,若不等式 ,若不等式 对任意的 对任意的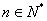 都成立,求实数 都成立,求实数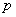 的取值范围. 的取值范围.
解 析(1)求得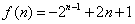 , , (过程略); (过程略);
(2)由(1)得,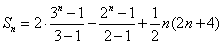 ,即 ,即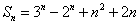 .因为不等式 .因为不等式 即 即 对任意的 对任意的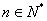 都成立,也就是 都成立,也就是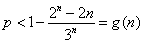 恒成立,所以 恒成立,所以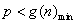 .于是问题转化为:当 .于是问题转化为:当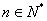 时,求 时,求 的最小值. 的最小值.
用差分法得,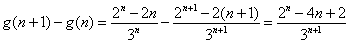 ,经验证知当 ,经验证知当 时, 时,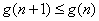 即 即 不增.下证明当 不增.下证明当 时, 时, 即 即 单调递增. 单调递增.
令 ,用差分法得, ,用差分法得, 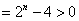 .所以当 .所以当 时, 时,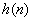 单调递增,所以 单调递增,所以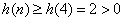 ,所以 ,所以 ,故当 ,故当 时, 时, 即 即 单调递增. 单调递增.
综上可知, ,故实数 ,故实数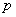 的取值范围是 的取值范围是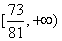 . .
例7用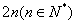 个相同的元件组成一个系统,有两种不同的连结方式,第一种是先串连后并联,如图1;第二种是先并连后串联,如图2.如果每个元件能否正常工作是相互独立的,且每个元件能正常工作的概率为 个相同的元件组成一个系统,有两种不同的连结方式,第一种是先串连后并联,如图1;第二种是先并连后串联,如图2.如果每个元件能否正常工作是相互独立的,且每个元件能正常工作的概率为 ,元件或系统能正常工作的概率通常称为可靠度.(1)分别求出图1和图2系统能正常工作的概率 ,元件或系统能正常工作的概率通常称为可靠度.(1)分别求出图1和图2系统能正常工作的概率 和 和 ;(2)请你比较一下哪个更可靠一些?并加以证明. ;(2)请你比较一下哪个更可靠一些?并加以证明.
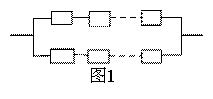 
解(1) , ,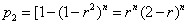 . .
(2) ,令 ,令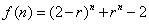 , ,
则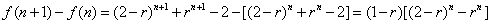 . .
因为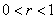 ,所以 ,所以 ,所以 ,所以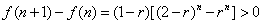 ,所以 ,所以 ,所以数列 ,所以数列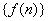 是递增数列,所以 是递增数列,所以 ,从而 ,从而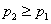 ,故系统2更可靠些. ,故系统2更可靠些.
点评 差分法实际上微分的离散形式,一阶差分就是离散函数中相邻两项之差,二阶差分就是一阶差分后所得新离散函数的一阶差分,多次差分就是多次求导的类比推广.导数是研究连续函数单调性和最值性的重要工具,同样差分法也是研究离散函数(数列)单调性和最值性的有效方法.
(责任编辑:admin) |
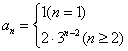 .
. .
. 对关于
对关于

