圆锥曲线上两点关于直线对称问题的解法
湖北省阳新县高级中学 邹生书
圆锥曲线上两点关于直线对称问题是高考命题的一个热点问题,该问题集中点弦、垂直、直线与圆锥曲线的位置关系、点与圆锥曲线的位置关系、方程函数不等式、点差法等重要数学知识和思想方法于一体,符合在知识网络交汇处、思想方法的交织线上和能力层次的交叉区内设置问题的命题特点,此类试题综合性强,但难度适中,对数学知识和能力的考查具有一定的深度,具有很好的选拔功能,是高考命题的热点.圆锥曲线上两点关于直线对称问题主要有联立方程和点差法两种解法,本文结合典型例题对这两种解法进行对比解读,供参考.
例1(2010年高考安徽卷理科第19题)椭圆 经过点 经过点 ,对称轴为坐标轴,焦点 ,对称轴为坐标轴,焦点 在 在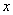 轴上,离心率 轴上,离心率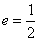 .(Ⅰ)求椭圆 .(Ⅰ)求椭圆 的方程;(Ⅱ)求 的方程;(Ⅱ)求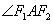 的平分线所在的直线 的平分线所在的直线 的方程;(Ⅲ)在椭圆上是否存在关于直线 的方程;(Ⅲ)在椭圆上是否存在关于直线 对称的相异两点?若存在,请找出;若不存在,说明理由. 对称的相异两点?若存在,请找出;若不存在,说明理由.
解(Ⅰ)椭圆 的方程为 的方程为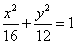 (过程略);(Ⅱ)直线 (过程略);(Ⅱ)直线 的方程为 的方程为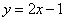 (过程略); (过程略);
(Ⅲ)法1(联立方程)假设在椭圆上存在关于直线 对称的相异两点 对称的相异两点 ,设线段 ,设线段 的中点为 的中点为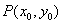 .因为直线 .因为直线 与直线 与直线 垂直,所以设直线 垂直,所以设直线 的方程为: 的方程为: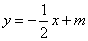 ,由此得 ,由此得 将其代入椭圆方程得, 将其代入椭圆方程得,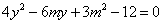 ①.因为 ①.因为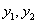 是此方程的两个根,所以 是此方程的两个根,所以 ,所以 ,所以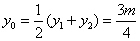 .又点 .又点 在直线 在直线 上,所以 上,所以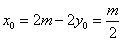 ,所以点 ,所以点 的坐标为 的坐标为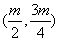 .又点 .又点 在直线 在直线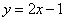 上,所以 上,所以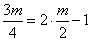 ,解得 ,解得 ,所以点 ,所以点 的坐标为 的坐标为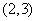 ,因为点 ,因为点 的坐标满足椭圆方程,所以点 的坐标满足椭圆方程,所以点 在椭圆上,不在椭圆内,故不存在这样的两点. 在椭圆上,不在椭圆内,故不存在这样的两点.
另解:将 代入①得, 代入①得,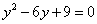 因方程有两个相等实根, 因方程有两个相等实根, 两点重合这与假设矛盾,故不存在这样的两点. 两点重合这与假设矛盾,故不存在这样的两点.
法2(点差法)假设在椭圆上存在关于直线 对称的相异两点 对称的相异两点 ,设线段 ,设线段 的中点为 的中点为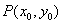 .因为 .因为 两点在椭圆上,故有 两点在椭圆上,故有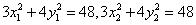 ,两式相减得, ,两式相减得, .又 .又 为线段 为线段 的中点,则有 的中点,则有 ,所以 ,所以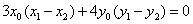 .因为直线 .因为直线 与直线 与直线 垂直,所以 垂直,所以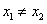 ,所以 ,所以 ,所以 ,所以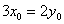 ①.又点 ①.又点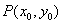 在直线 在直线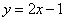 上,所以 上,所以 ②. ②.
解①②得点 的坐标为 的坐标为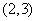 ,因为点 ,因为点 的坐标满足椭圆方程,所以点 的坐标满足椭圆方程,所以点 在椭圆上,不在椭圆内,故不存在这样的两点. 在椭圆上,不在椭圆内,故不存在这样的两点.
点评 本题第三问是一道探究椭圆上是否存在关于已知直线对称的相异两点的存在性探索题,既可用方程思想求解也可用点差法解答,因为答案是不存在,所以最后的关键是找出矛盾,这个矛盾既可以是假设相异的两点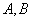 重合,也可以是线段 重合,也可以是线段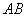 的中点 的中点 在椭圆上,不在椭圆内. 在椭圆上,不在椭圆内.
例2 已知椭圆中心在原点,焦点在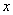 轴上,一个顶点的坐标为 轴上,一个顶点的坐标为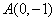 ,且其右焦点到直线 ,且其右焦点到直线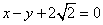 的距离为 的距离为 .(1)求椭圆的方程;(2)是否存在斜率为 .(1)求椭圆的方程;(2)是否存在斜率为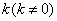 的直线 的直线 ,使 ,使 与已知曲线交于不同的两点 与已知曲线交于不同的两点 ,且有 ,且有 .若存在,求 .若存在,求 的取值范围;若不存,请说明理由. 的取值范围;若不存,请说明理由.
解 (1)求得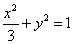 (过程略); (过程略);
(2)法1(联立方程)设直线 的方程为 的方程为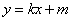 ,将其代入椭圆方程得 ,将其代入椭圆方程得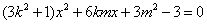 .设 .设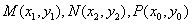 ,则 ,则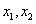 方程的两个根,故 方程的两个根,故 .因点 .因点 在直线 在直线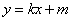 上,所以 上,所以 .又点 .又点 在椭圆内,所以有 在椭圆内,所以有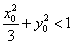 ,即 ,即 ,化简得 ,化简得 ①. ①.
又 ,所以 ,所以 ,即 ,即 ,化简得 ,化简得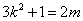 ②.由①②消去 ②.由①②消去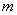 得, 得, ,又 ,又 ,所以 ,所以 的取值范围是 的取值范围是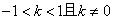 . .
法2(点差法)假设存在这样的直线 ,设点 ,设点 为线段 为线段 的中点,设 的中点,设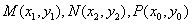 ,则 ,则 ,因为点 ,因为点 在椭圆上,所以 在椭圆上,所以 ,两式相减得, ,两式相减得,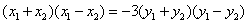 ,即 ,即 ,所以 ,所以 ,即 ,即 ①.又 ①.又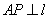 ,所以 ,所以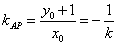 ,则 ,则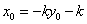 ②.由①②得 ②.由①②得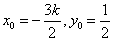 ,所以 ,所以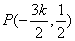 , ,
又因为点 在椭圆内,所以有 在椭圆内,所以有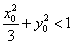 ,即 ,即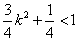 ,解得 ,解得 ,又 ,又 , ,
所以 的取值范围是 的取值范围是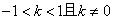 . .
例3试确定实数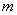 的取值范围,使抛物线 的取值范围,使抛物线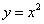 上存在两点关于直线 上存在两点关于直线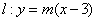 对称. 对称.
法1(联立方程)因为设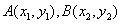 为抛物线上关于 为抛物线上关于 对称的两个点,设线段 对称的两个点,设线段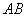 的中点为 的中点为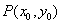 . .
又直线 与直线 与直线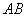 垂直,故可设直线 垂直,故可设直线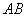 的方程为 的方程为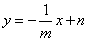 ,将其代入 ,将其代入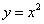 得 得 .因为 .因为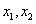 是该方程的两个根,故 是该方程的两个根,故 .又点 .又点 在直线 在直线 上,所以 上,所以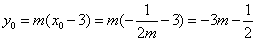 ,又因为点 ,又因为点 在抛物线内,所以 在抛物线内,所以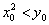 即 即 ,也就是 ,也就是 , , ,又 ,又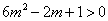 恒成立,所以 恒成立,所以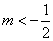 . .
法2(点差法)显然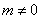 ,设 ,设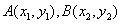 为抛物线上关于 为抛物线上关于 对称的两个点,设线段 对称的两个点,设线段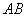 的中点为 的中点为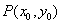 .则 .则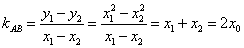 ,又直线 ,又直线 与直线 与直线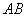 垂直,所以 垂直,所以 ,即 ,即 .下同法1略. .下同法1略.
例4(06年高考福建卷)已知椭圆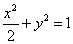 的左焦点为 的左焦点为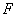 , ,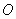 为坐标原点.(1)求过点 为坐标原点.(1)求过点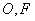 ,并且与椭圆的左准线 ,并且与椭圆的左准线 相切的圆的方程;(2)设过点 相切的圆的方程;(2)设过点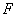 且不与坐标轴垂直的直线交椭圆于 且不与坐标轴垂直的直线交椭圆于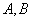 两点,线段 两点,线段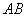 的垂直平分线与 的垂直平分线与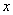 轴交于点 轴交于点 ,求点 ,求点 的横坐标的取值范围. 的横坐标的取值范围.
解(1)略;(2)法1(联立方程)设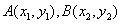 ,设 ,设 为线段 为线段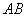 的中点,设过左焦点 的中点,设过左焦点 且不与坐标轴垂直的直线 且不与坐标轴垂直的直线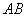 的方程为 的方程为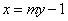 ,将其代入椭圆方程整理得, ,将其代入椭圆方程整理得, .因为 .因为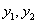 是方程的两个根,所以 是方程的两个根,所以 .又点 .又点 在直线 在直线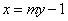 上,所以 上,所以 ,故点 ,故点 的坐标为 的坐标为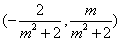 .又 .又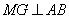 ,所以 ,所以 ,故直线 ,故直线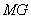 的点斜式方程为 的点斜式方程为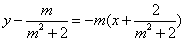 .令 .令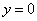 得, 得,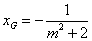 ,又 ,又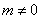 ,所以 ,所以 ,故点 ,故点 的横坐标的取值范围是 的横坐标的取值范围是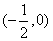 . .
法2(点差法)设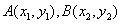 ,则有 ,则有 ,两式相减得, ,两式相减得,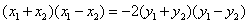 .又设 .又设 为线段 为线段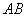 的中点,则有 的中点,则有 ,所以 ,所以 .因为 .因为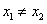 ,所以 ,所以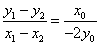 ,即 ,即 ,所以线段 ,所以线段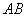 的垂直平分线的点斜式方程为 的垂直平分线的点斜式方程为 ,令 ,令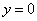 得点 得点 的横向坐标为 的横向坐标为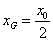 .又 .又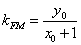 ,所以 ,所以 ,即 ,即 ,又 ,又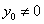 所以 所以 即 即 ,故点 ,故点 的横坐标的取值范围是 的横坐标的取值范围是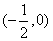 . .
评注 本题因直线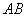 过左焦点 过左焦点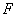 ,线段 ,线段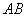 的中点 的中点 必在椭圆内,故需另寻它法求范围.法1用函数值域求范围,法2用不等式求范围. 必在椭圆内,故需另寻它法求范围.法1用函数值域求范围,法2用不等式求范围.
综上可知,解决圆锥曲线上两点关于直线对称问题,要充分利用“垂直”与“中点”这两个条件,“联立方程”和“点差法”只是将这两个几何条件代数化的一种途径,“主动设点(设弦端点坐标、设弦中点坐标)设线(设直线方程)、引入多元设而不求”是解决这类问题的基本方法和必由之路。问题解决既要有整体思想又要有目标意识和对多元的驾驭能力,对学生的综合能力的考查达到了一定的高度.“联立方程”方法基础传统,“点差法”设点作差是解决中点弦问题的较为特殊的经典方法,在解题教学中要指导学生亲手尝试、切身感悟自我反思总结提炼.
参考文献:
邹生书.点差法与向量联手简解中点弦问题.中学数学,2011(5)
(责任编辑:admin) |

 ,化简得
,化简得
