|
用“一分为二”的观点看待函数问题 湖北省阳新县高级中学 邹生书 毛泽东同志曾指出:“一分为二，这是个普遍的现象，这就是辩证法.”若用一分为二的观点看待数学问题，则可使一些数学问题峰回路转柳暗花明.本文笔者试图通过典型例题来诠释一分为二的观点在解决函数问题中的指导作用，从中体验“一分为二”既相互对立又相互联系和统一的辩证关系. 一、对函数自变量的取值范围一分为二 例1（2010年高考全国卷Ⅰ第20题）已知函数  .（1）若 ，求 的取值范围；（2）证明: .分析 （1）略；（2）对自变量的取值范围一分为二，则只要证：①当  时， ；②当 时， .证明 ①当 时， ，所以 在 上单调递增，所以 ，所以，当且仅当 时等号成立.②当 时，因为 ，所以 ，所以 在 上单调递减，所以 ，从而在上单调递增，所以 ，故当时，.综上可知 .点评 对自变量的取值范围一分为二实际上就是分类讨论的思想. 例2(2011年高考浙江卷理科第22题)设函数  .（1）若 为 的极值点，求实数；（2）求实数的取值范围，使得对任意的 ，恒有 成立.分析 对于第(2)问，注意到，当  时，不等式恒成立，因而问题等价于当 时，不等式 恒成立，求实数的取值范围. 由 可分离参数，转化为当时，不等式 及 都恒成立.于是问题转化为求函数 的最大值及函数 的最小值，易求得的取值范围是 .点评 本题先将自变量的取值一分为二，再用分离参数法将函数一分为二. 二、对函数解析式一分为二成两种类型的函数 例3 讨论函数  的零点个数.解析 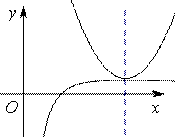要讨论函数 的零点个数，按对数型和二次函数将该函数一分为二，则只要讨论两函数 图像的交点个数即可.由于 ，当 时， ， 单调递增；当 时， ，单调递减，所以 .又 时， ；当 时， .而 ，在同一坐标系画出这两个函数的图像如图所示. 从图像可知： （1）当  即 时，两函数图像只有一个公共点，则只有一个零点；（2）当  即 时，两函数的图像没有公共点，则没有零点；（3）当  即 时，两函数图像有两个公共点，则有两个零点.例4 求证:对任意的  ，都有 . 分析 设  ，利用导数求最小值，只要证明 即可.易求得 ，然而很难求出 的零点，故可考虑按指数、对数的形式将函数一分为二成两个函数 ，从这两个函数的图像和最值寻找解题契机. 解 设 ，则只要证明 即可. ，当 时， ；当  时， ，所以 .因为 ，当  时，；当 时，，所以  .因此， .因为两个等号成立的条件分别是 和，故两个等号不能同时成立，所以.这两个函数的图像如图所示.三、将函数一分为二成两个函数之积 例5（2011年湖南卷理科第22题）已知函数  .（Ⅰ）求函数 的零点个数，并说明理由；（Ⅱ）略.解 因函数  ，故 零点的集合就是函数 在 上零点集合之并.显然 有一个零点 ，又 ，由零存在性定理知， 在 上有零点，又 在 上单调递增，故在上有唯一零点.综上所述，函数有两个零点.例6（2010年江西高考题）等比数列  中， ，函数 ，则 （ ）    解 设  ，则 ，所以 ，所以 ，故选 .四、对导函数一分为二成两个函数之和 例7 证明:对任意的正整数  ，不等式 都成立.分析 对任意的正整数 ，要证不等式都成立，设 ，则只要证明当时，不等式 即 恒成立.设 ，则只要证当时， 恒成立即可.证明 设  .则当时，  ，所以在 上单调递增，所以当时， ，即，也就是恒成立.令 ，则 ，故对任意的正整数，不等式都成立.点评 这里判断导函数 的符号时，其分子不能用因式分解法定号，我们将分子 一分为二成两个非负数之和 ，从而确定导函数的符号，使问题得以解决.例8讨论函数 的零点个数.解  ，注意到 ，且当时，，单调递增；当时，，单调递减，所以 .又时， ；当时， .由函数的图像可知：（1）当  即时，函数的图像与 轴只有一个公共点，所以只有一个零点；（2）当  即时，函数的图像与轴没有公共点，所以没有零点；（3）当  即时，函数的图像与轴有两个公共点，所以有两个零点.点评 这里将导函数一分为二成两个函数  与 之和，而这两个函数具有相同的零点和相同的单调性，从而得出导函数零点和单调性，本解法充分体现了一分为二的对立与统一.一分为二是普遍的，但不能作机械的理解.本文所举案例中的函数的可分性从内容、形式及过程是多种多样的，既可对自变量的取值范围一分为二，也可将一个函数整体一分为二成两个函数的和差积商，还可对其导函数或其局部一分为二.一分为二只是一种形式，正确地认识和把握一分为二，就既要看到矛盾双方的对立和排斥，也要看到双方的联系和统一，以及在一定条件下的相互转化，对立和统一才是一分为二的精髓. (责任编辑：admin) |