|
高中数学竞赛讲义（一） ──集合与简易逻辑 一、基础知识 定义1 一般地，一组确定的、互异的、无序的对象的全体构成集合，简称集，用大写字母来表示；集合中的各个对象称为元素，用小写字母来表示，元素  在集合A中，称属于A，记为 ，否则称不属于A，记作 。例如，通常用N，Z，Q，B，Q+分别表示自然数集、整数集、有理数集、实数集、正有理数集，不含任何元素的集合称为空集，用 来表示。集合分有限集和无限集两种。集合的表示方法有列举法：将集合中的元素一一列举出来写在大括号内并用逗号隔开表示集合的方法，如{1，2，3}；描述法：将集合中的元素的属性写在大括号内表示集合的方法。例如{有理数}，  分别表示有理数集和正实数集。定义2 子集：对于两个集合A与B，如果集合A中的任何一个元素都是集合B中的元素，则A叫做B的子集，记为  ，例如 。规定空集是任何集合的子集，如果A是B的子集，B也是A的子集，则称A与B相等。如果A是B的子集，而且B中存在元素不属于A，则A叫B的真子集。定义3 交集，  定义4 并集，  定义5 补集，若  称为A在I中的补集。定义6 差集，  。定义7 集合  记作开区间 ，集合 记作闭区间 ，R记作 定理1 集合的性质：对任意集合A，B，C，有： （1）  （2） ；（3）  （4） 【证明】这里仅证（1）、（3），其余由读者自己完成。 （1）若  ，则，且 或 ，所以 或 ，即 ；反之，，则或，即且或，即且 ，即 （3）若  ，则 或 ，所以或 ，所以 ，又 ，所以 ，即 ，反之也有 定理2 加法原理：做一件事有  类办法，第一类办法中有 种不同的方法，第二类办法中有 种不同的方法，…，第类办法中有 种不同的方法，那么完成这件事一共有 种不同的方法。定理3 乘法原理：做一件事分 个步骤，第一步有种不同的方法，第二步有种不同的方法，…，第步有种不同的方法，那么完成这件事一共有 种不同的方法。二、方法与例题 1．利用集合中元素的属性，检验元素是否属于集合。 例1 设  ，求证：（1）  ；（2）  ；（3）若  ，则 [证明]（1）因为  ，且 ，所以 （2）假设  ，则存在 ，使 ，由于 和 有相同的奇偶性，所以 是奇数或4的倍数，不可能等于 ，假设不成立，所以 （3）设  ，则   （因为  ）。2．利用子集的定义证明集合相等，先证 ，再证 ，则A=B。例2 设A，B是两个集合，又设集合M满足  ，求集合M（用A，B表示）。【解】先证  ，若，因为 ，所以 ，所以； 再证  ，若 ，则 1）若，则 ；2）若，则 。所以 综上，  3．分类讨论思想的应用。 例3  ，若 ，求 【解】依题设，  ，再由 解得 或 ，因为  ，所以，所以 ，所以 或2，所以 或3。因为  ，所以 ，若 ，则 ，即 ，若 ，则 或 ，解得 综上所述， 或 ； 或。4．计数原理的应用。 例4 集合A，B，C是I={1，2，3，4，5，6，7，8，9，0}的子集，（1）若  ，求有序集合对（A，B）的个数；（2）求I的非空真子集的个数。【解】（1）集合I可划分为三个不相交的子集；A\B，B\A，  中的每个元素恰属于其中一个子集，10个元素共有310种可能，每一种可能确定一个满足条件的集合对，所以集合对有310个。（2）I的子集分三类：空集，非空真子集，集合I本身，确定一个子集分十步，第一步，1或者属于该子集或者不属于，有两种；第二步，2也有两种，…，第10步，0也有两种，由乘法原理，子集共有  个，非空真子集有1022个。5．配对方法。 例5 给定集合  的 个子集： ，满足任何两个子集的交集非空，并且再添加I的任何一个其他子集后将不再具有该性质，求的值。【解】将I的子集作如下配对：每个子集和它的补集为一对，共得  对，每一对不能同在这个子集中，因此， ；其次，每一对中必有一个在这个子集中出现，否则，若有一对子集未出现，设为C1A与A，并设 ，则 ，从而可以在个子集中再添加 ，与已知矛盾，所以 。综上， 。6．竞赛常用方法与例问题。 定理4 容斥原理；用  表示集合A的元素个数，则  ，需要xy此结论可以推广到个集合的情况，即   定义8 集合的划分：若  ，且 ，则这些子集的全集叫I的一个-划分。定理5 最小数原理：自然数集的任何非空子集必有最小数。 定理6 抽屉原理：将  个元素放入 个抽屉，必有一个抽屉放有不少于 个元素，也必有一个抽屉放有不多于 个元素；将无穷多个元素放入个抽屉必有一个抽屉放有无穷多个元素。例6 求1，2，3，…，100中不能被2，3，5整除的数的个数。 【解】 记  ， ，由容斥原理，  ，所以不能被2，3，5整除的数有 个。例7 S是集合{1，2，…，2004}的子集，S中的任意两个数的差不等于4或7，问S中最多含有多少个元素？ 【解】将任意连续的11个整数排成一圈如右图所示。由题目条件可知每相邻两个数至多有一个属于S，将这11个数按连续两个为一组，分成6组，其中一组只有一个数，若S含有这11个数中至少6个，则必有两个数在同一组，与已知矛盾，所以S至多含有其中5个数。又因为2004=182×11+2，所以S一共至多含有182×5+2=912个元素，另一方面，当  时，恰有 ，且S满足题目条件，所以最少含有912个元素。例8 求所有自然数  ，使得存在实数 满足： 【解】 当  时， ；当 时， ；当 时，  。下证当 时，不存在满足条件。令  ，则 所以必存在某两个下标  ，使得 ，所以 或 ，即 ，所以 或 ，。（ⅰ）若 ，考虑 ，有 或 ，即 ，设 ，则 ，导致矛盾，故只有 考虑  ，有 或 ，即 ，设，则 ，推出矛盾，设，则 ，又推出矛盾， 所以 故当时，不存在满足条件的实数。（ⅱ）若  ，考虑，有 或 ，即 ，这时 ，推出矛盾，故 。考虑，有或  ，即=3，于是 ，矛盾。因此 ，所以 ，这又矛盾，所以只有 ，所以。故当时，不存在满足条件的实数。例9 设A={1，2，3，4，5，6}，B={7，8，9，……，n}，在A中取三个数，B中取两个数组成五个元素的集合  ， 求的最小值。【解】  设B中每个数在所有 中最多重复出现次，则必有 。若不然，数出现次（ ），则 在出现的所有中，至少有一个A中的数出现3次，不妨设它是1，就有集合{1， } ，其中 ，为满足题意的集合。 必各不相同，但只能是2，3，4，5，6这5个数，这不可能，所以 20个 中，B中的数有40个，因此至少是10个不同的，所以 。当 时，如下20个集合满足要求：{1，2，3，7，8}， {1，2，4，12，14}， {1，2，5，15，16}， {1，2，6，9，10}， {1，3，4，10，11}， {1，3，5，13，14}， {1，3，6，12，15}， {1，4，5，7，9}， {1，4，6，13，16}， {1，5，6，8，11}， {2，3，4，13，15}， {2，3，5，9，11}， {2，3，6，14，16}， {2，4，5，8，10}， {2，4，6，7，11}， {2，5，6，12，13}， {3，4，5，12，16}， {3，4，6，8，9}， {3，5，6，7，10}， {4，5，6，14，15}。 例10 集合{1，2，…，3n}可以划分成 个互不相交的三元集合 ，其中 ，求满足条件的最小正整数 【解】 设其中第  个三元集为 则1+2+…+ 所以  。当为偶数时，有 ，所以 ，当为奇数时，有 ，所以，当 时，集合{1，11，4}，{2，13，5}，{3，15，6}，{9，12，7}，{10，14，8}满足条件，所以的最小值为5。三、基础训练题 1．给定三元集合  ，则实数的取值范围是___________。2．若集合  中只有一个元素，则 =___________。3．集合  的非空真子集有___________个。4．已知集合  ，若 ，则由满足条件的实数组成的集合P=___________。5．已知  ，且，则常数的取值范围是___________。6．若非空集合S满足  ，且若 ，则 ，那么符合要求的集合S有___________个。7．集合  之间的关系是___________。8．若集合  ，其中 ， 且 ，若 ，则A中元素之和是___________。9．集合  ，且 ，则满足条件的值构成的集合为___________。10．集合  ，则 ___________。11．已知S是由实数构成的集合，且满足1）  ）若，则 。如果 ，S中至少含有多少个元素？说明理由。12．已知  ，又C为单元素集合，求实数的取值范围。四、高考水平训练题 1．已知集合 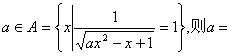 ，且A=B，则 ___________， ___________。2．   ，则 ___________。3．已知集合  ，当 时，实数的取值范围是___________。4．若实数 为常数，且 ___________。5．集合  ，若 ，则 ___________。6．集合  ，则 中的最小元素是___________。7．集合  ，且A=B，则 ___________。8．已知集合  ，且，则 的取值范围是___________。9．设集合   ，问：是否存在 ，使得 ，并证明你的结论。10．集合A和B各含有12个元素， 含有4个元素，试求同时满足下列条件的集合C的个数：1） 且C中含有3个元素；2） 。11．判断以下命题是否正确：设A，B是平面上两个点集，  ，若对任何 ，都有 ，则必有，证明你的结论。五、联赛一试水平训练题 1．已知集合 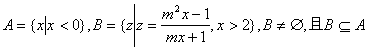 ，则实数的取值范围是___________。2．集合  的子集B满足：对任意的 ，则集合B中元素个数的最大值是___________。3．已知集合  ，其中 ，且 ，若P=Q，则实数 ___________。4．已知集合  ，若是平面上正八边形的顶点所构成的集合，则 ___________。5．集合  ，集合 ，则集合M与N的关系是___________。6．设集合  ，集合A满足： ，且当时， ，则A中元素最多有___________个。7．非空集合  ，≤则使 成立的所有的集合是___________。8．已知集合A，B，aC（不必相异）的并集  , 则满足条件的有序三元组（A，B，C）个数是___________。9．已知集合  ，问：当取何值时， 为恰有2个元素的集合？说明理由，若改为3个元素集合，结论如何？10．求集合B和C，使得  ，并且C的元素乘积等于B的元素和。11．S是Q的子集且满足：若  ，则 恰有一个成立，并且若 ，则 ，试确定集合S。12．集合S={1，2，3，4，5，6，7，8，9，0}的若干个五元子集满足：S中的任何两个元素至多出现在两个不同的五元子集中，问：至多有多少个五元子集？ 六、联赛二试水平训练题 1．  是三个非空整数集，已知对于1，2，3的任意一个排列 ，如果 ， ，则 。求证：中必有两个相等。2．求证：集合{1，2，…，1989}可以划分为117个互不相交的子集  ，使得（1）每个恰有17个元素；（2）每个中各元素之和相同。3．某人写了 封信，同时写了个信封，然后将信任意装入信封，问：每封信都装错的情况有多少种？4．设  是20个两两不同的整数，且整合 中有201个不同的元素，求集合 中不同元素个数的最小可能值。5．设S是由  个人组成的集合。求证：其中必定有两个人，他们的公共朋友的个数为偶数。6．对于整数  ，求出最小的整数 ，使得对于任何正整数，集合 的任一个元子集中，均有至少3个两两互质的元素。7．设集合S={1，2，…，50}，求最小自然数 ，使S的任意一个 元子集中都存在两个不同的数a和b，满足 。8．集合  ，试作出X的三元子集族&，满足：（1）X的任意一个二元子集至少被族&中的一个三元子集包含； （2）  。9．设集合  ，求最小的正整数，使得对A的任意一个14-分划 ，一定存在某个集合 ，在中有两个元素a和b满足 。本系列讲座由在人教中数论坛网友“0.1”整理提供，感谢他（她）的分享。 (责任编辑：admin) |