高中数学精神讲义（二）_高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网-中学学科网

    高中数学精神讲义（二）
    ──二次函数与命题
    一、基础知识
    1．二次函数：当0时，y=ax²+bx+c或f(x)=ax²+bx+c称为关于x的二次函数，其对称轴为直线x=-，另外配方可得f(x)=a(x-x₀)²+f(x₀)，其中x₀=-，下同。
    2．二次函数的性质：当a>0时，f(x)的图象开口向上，在区间（-∞，x₀]上随自变量x增大函数值减小（简称递减），在[x₀, -∞）上随自变量增大函数值增大（简称递增）。当a<0时，情况相反。
    3．当a>0时，方程f(x)=0即ax²+bx+c=0…①和不等式ax²+bx+c>0…②及ax²+bx+c<0…③与函数f(x)的关系如下（记△=b²-4ac）。
    1）当△>0时，方程①有两个不等实根，设x₁,x₂(x₁<x₂)，不等式②和不等式③的解集分别是{x|x<x₁或x>x₂}和{x|x₁<x<x₂}，二次函数f(x)图象与x轴有两个不同的交点，f(x)还可写成f(x)=a(x-x₁)(x-x₂).
    2）当△=0时，方程①有两个相等的实根x₁=x₂=x₀=,不等式②和不等式③的解集分别是{x|x}和空集，f(x)的图象与x轴有唯一公共点。
    3）当△<0时，方程①无解，不等式②和不等式③的解集分别是R和.f(x)图象与x轴无公共点。
    当a<0时，请读者自己分析。
    4．二次函数的最值：若a>0，当x=x₀时，f(x)取最小值f(x₀)=,若a<0，则当x=x₀=时，f(x)取最大值f(x₀)=.对于给定区间[m,n]上的二次函数f(x)=ax²+bx+c(a>0)，当x₀∈[m, n]时，f(x)在[m, n]上的最小值为f(x₀); 当x₀<m时。f(x)在[m, n]上的最小值为f(m)；当x₀>n时，f(x)在[m, n]上的最小值为f(n)（以上结论由二次函数图象即可得出）。
    定义1 能判断真假的语句叫命题，如“3>5”是命题，“萝卜好大”不是命题。不含逻辑联结词“或”、“且”、“非”的命题叫做简单命题，由简单命题与逻辑联结词构成的命题由复合命题。
    注1 “p或q”复合命题只有当p，q同为假命题时为假，否则为真命题；“p且q”复合命题只有当p，q同时为真命题时为真，否则为假命题；p与“非p”即“p”恰好一真一假。
    定义2 原命题：若p则q（p为条件，q为结论）；逆命题：若q则p；否命题：若非p则q；逆否命题：若非q则非p。
    注2 原命题与其逆否命题同真假。一个命题的逆命题和否命题同真假。
    注3 反证法的理论依据是矛盾的排中律，而未必是证明原命题的逆否命题。
    定义3 如果命题“若p则q”为真，则记为pq否则记作pq.在命题“若p则q”中，如果已知pq,则p是q的充分条件；如果qp，则称p是q的必要条件；如果pq但q不p，则称p是q的充分非必要条件；如果p不q但pq，则p称为q的必要非充分条件；若pq且qp，则p是q的充要条件。
    二、方法与例题
    1．待定系数法。
    例1 设方程x²-x+1=0的两根是α，β，求满足f(α)=β,f(β)=α,f(1)=1的二次函数f(x).
    【解】设f(x)=ax²+bx+c(a0),
    则由已知f(α)=β,f(β)=α相减并整理得（α-β）[（α+β）a+b+1]=0，
    因为方程x²-x+1=0中△0，
    所以αβ，所以(α+β)a+b+1=0.
    又α+β=1,所以a+b+1=0.
    又因为f(1)=a+b+c=1，
    所以c-1=1，所以c=2.
    又b=-(a+1)，所以f(x)=ax²-(a+1)x+2.
    再由f(α)=β得aα²-(a+1)α+2=β,
    所以aα²-aα+2=α+β=1，所以aα²-aα+1=0.
    即a(α²-α+1)+1-a=0,即1-a=0，
    所以a=1,
    所以f(x)=x²-2x+2.
    2．方程的思想。
    例2 已知f(x)=ax²-c满足-4≤f(1)≤-1, -1≤f(2)≤5，求f(3)的取值范围。
    【解】因为-4≤f(1)=a-c≤-1,
    所以1≤-f(1)=c-a≤4.
    又-1≤f(2)=4a-c≤5, f(3)=f(2)-f(1),
    所以×(-1)+≤f(3)≤×5+×4,
    所以-1≤f(3)≤20.
    3．利用二次函数的性质。
    例3 已知二次函数f(x)=ax²+bx+c(a,b,c∈R, a0)，若方程f(x)=x无实根，求证：方程f(f(x))=x也无实根。
    【证明】若a>0，因为f(x)=x无实根，所以二次函数g(x)=f(x)-x图象与x轴无公共点且开口向上，所以对任意的x∈R,f(x)-x>0即f(x)>x，从而f(f(x))>f(x)。
    所以f(f(x))>x，所以方程f(f(x))=x无实根。
    注：请读者思考例3的逆命题是否正确。
    4．利用二次函数表达式解题。
    例4 设二次函数f(x)=ax²+bx+c(a>0)，方程f(x)=x的两根x₁, x₂满足0<x₁<x₂<,
    （Ⅰ）当x∈(0, x₁)时，求证：x<f(x)<x₁；
    （Ⅱ）设函数f(x)的图象关于x=x₀对称，求证：x₀<
    【证明】因为x₁, x₂是方程f(x)-x=0的两根，所以f(x)-x=a(x-x₁)(x-x₂)，
    即f(x)=a(x-x₁)(x-x₂)+x.
    （Ⅰ）当x∈(0, x₁)时，x-x₁<0, x-x₂<0, a>0，所以f(x)>x.
    其次f(x)-x₁=(x-x₁)[a(x-x₂)+1]=a(x-x₁)[x-x₂+]<0，所以f(x)<x₁.
    综上，x<f(x)<x₁.
    （Ⅱ）f(x)=a(x-x₁)(x-x₂)+x=ax₂+[1-a(x₁+x₂)]x+ax₁x₂,
    所以x₀=,
    所以，
    所以
    5．构造二次函数解题。
    例5 已知关于x的方程(ax+1)²=a²(a-x²), a>1，求证：方程的正根比1小，负根比-1大。
    【证明】方程化为2a²x²+2ax+1-a²=0.
    构造f(x)=2a²x²+2ax+1-a²,
    f(1)=(a+1)²>0, f(-1)=(a-1)²>0, f(0)=1-a²<0, 即△>0，
    所以f(x)在区间（-1,0）和（0，1）上各有一根。
    即方程的正根比1小，负根比-1大。
    6．定义在区间上的二次函数的最值。
    例6 当x取何值时，函数y=取最小值？求出这个最小值。
    【解】 y=1-,令u,则0<u≤1。
    y=5u²-u+1=5,
    且当即x=3时，y_min=.
    例7 设变量x满足x²+bx≤-x(b<-1)，并且x²+bx的最小值是，求b的值。
    【解】由x²+bx≤-x(b<-1)，得0≤x≤-(b+1).
    ⅰ)-≤-(b+1)，即b≤-2时，x²+bx的最小值为-，所以b²=2，所以（舍去）。
    ⅱ) ->-(b+1)，即b>-2时，x²+bx在[0，-(b+1)]上是减函数，
    所以x²+bx的最小值为b+1,b+1=-,b=-.
    综上，b=-.
    7.一元二次不等式问题的解法。
    例8 已知不等式组 ①②的整数解恰好有两个，求a的取值范围。
    【解】因为方程x²-x+a-a²=0的两根为x₁=a, x₂=1-a,
    若a≤0，则x₁<x₂.①的解集为a<x<1-a，由②得x>1-2a.
    因为1-2a≥1-a，所以a≤0,所以不等式组无解。
    若a>0，ⅰ）当0<a<时，x₁<x₂,①的解集为a<x<1-a.
    因为0<a<x<1-a<1，所以不等式组无整数解。
    ⅱ）当a=时，a=1-a，①无解。
    ⅲ）当a>时，a>1-a，由②得x>1-2a，
    所以不等式组的解集为1-a<x<a.
    又不等式组的整数解恰有2个，
    所以a-(1-a)>1且a-(1-a)≤3，
    所以1<a≤2，并且当1<a≤2时，不等式组恰有两个整数解0，1。
    综上，a的取值范围是1<a≤2.
    8．充分性与必要性。
    例9 设定数A，B，C使得不等式
    A(x-y)(x-z)+B(y-z)(y-x)+C(z-x)(z-y)≥0    ①
    对一切实数x,y,z都成立，问A，B，C应满足怎样的条件？（要求写出充分必要条件，而且限定用只涉及A，B，C的等式或不等式表示条件）
    【解】充要条件为A，B，C≥0且A²+B²+C²≤2(AB+BC+CA).
    先证必要性，①可改写为A(x-y)²-(B-A-C)(y-z)(x-y)+C(y-z)²≥0   ②
    若A=0，则由②对一切x,y,z∈R成立，则只有B=C，再由①知B=C=0，若A0，则因为②恒成立，所以A>0，△=(B-A-C)²(y-z)²-4AC(y-z)²≤0恒成立，所以(B-A-C)²-4AC≤0，即A²+B²+C²≤2(AB+BC+CA)
    同理有B≥0，C≥0，所以必要性成立。
    再证充分性，若A≥0，B≥0，C≥0且A²+B²+C²≤2(AB+BC+CA)，
    1）若A=0，则由B²+C²≤2BC得(B-C)²≤0，所以B=C，所以△=0，所以②成立，①成立。
    2）若A>0，则由③知△≤0，所以②成立，所以①成立。
    综上，充分性得证。
    9．常用结论。
    定理1 若a, b∈R, |a|-|b|≤|a+b|≤|a|+|b|.
    【证明】因为-|a|≤a≤|a|,-|b|≤b≤|b|，所以-(|a|+|b|)≤a+b≤|a|+|b|,
    所以|a+b|≤|a|+|b|（注：若m>0，则-m≤x≤m等价于|x|≤m）.
    又|a|=|a+b-b|≤|a+b|+|-b|,
    即|a|-|b|≤|a+b|.综上定理1得证。
    定理2 若a,b∈R, 则a²+b²≥2ab；若x,y∈R⁺,则x+y≥
    (证略)
    注定理2可以推广到n个正数的情况，在不等式证明一章中详细论证。
    三、基础训练题
    1．下列四个命题中属于真命题的是________，①“若x+y=0，则x、y互为相反数”的逆命题；②“两个全等三角形的面积相等”的否命题；③“若q≤1，则x²+x+q=0有实根”的逆否命题；④“不等边三角形的三个内角相等”的逆否命题。
    2．由上列各组命题构成“p或q”，“p且q”，“非p”形式的复合命题中，p或q为真，p且q为假，非p为真的是_________.①p；3是偶数，q：4是奇数；②p:3+2=6,q:③p:a∈(a,b),q:{a}{a,b}; ④ p: QR, q: N=Z.
    3. 当|x-2|<a时，不等式|x²-4|<1成立，则正数a的取值范围是________.
    4. 不等式ax²+(ab+1)x+b>0的解是1<x<2，则a, b的值是____________.
    5. x1且x2是x-1的__________条件，而-2<m<0且0<n<1是关于x的方程x²+mx+n=0有两个小于1的正根的__________条件.
    6.命题“垂直于同一条直线的两条直线互相平行”的逆命题是_________.
    7.若S={x|mx²+5x+2=0}的子集至多有2个，则m的取值范围是_________.
    8. R为全集，A={x|3-x≥4}, B=, 则(C_RA)∩B=_________.
    9. 设a, b是整数，集合A={(x,y)|(x-a)²+3b≤6y}，点（2，1）∈A，但点（1，0）A，（3，2）A则a,b的值是_________.
    10．设集合A={x||x|<4}, B={x|x²-4x+3>0}，则集合{x|x∈A且xA∩B}=_________.
    11. 求使不等式ax²+4x-1≥-2x²-a对任意实数x恒成立的a的取值范围。
    12．对任意x∈[0,1],有 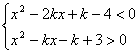①②成立，求k的取值范围。
    四、高考水平训练题
    1．若不等式|x-a|<x的解集不空，则实数a的取值范围是_________.
    2．使不等式x²+(x-6)x+9>0当|a|≤1时恒成立的x的取值范围是_________.
    3．若不等式-x²+kx-4<0的解集为R，则实数k的取值范围是_________.
    4．若集合A={x||x+7|>10}, B={x||x-5|<k}，且A∩B=B，则k的取值范围是_________.
    5．设a₁、a₂, b₁、b₂, c₁、c₂均为非零实数，不等式a₁x²+b₁x+c₁>0和a₂x²+b₂x+c₂>0解集分别为M和N，那么“”是“M=N”的_________条件。
    6．若下列三个方程x²+4ax-4a+3=0, x²+(a-1)x+a²=0, x²+2ax-2a=0中至少有一个方程有实根，则实数a的取值范围是_________.
    7．已知p, q都是r的必要条件，s是r的充分条件，q是s的充分条件，则r是q的_________条件。
    8．已知p: |1-|≤2, q: x²-2x+1-m²≤0(m>0)，若非p是非q的必要不充分条件，则实数m的取值范围是_________.
    9．已知a>0，f(x)=ax²+bx+c，对任意x∈R有f(x+2)=f(2-x)，若f(1-2x²)<f(1+2x-x²)，求x 的取值范围。
    10．已知a, b, c∈R, f(x)=ax²+bx+c, g(x)=ax+b, 当|x|≤1时，|f(x)|≤1,
    (1)求证：|c|≤1;
    (2)求证：当|x|≤1时，|g(x)|≤2;
    (3)当a>0且|x|≤1时，g(x)最大值为2，求f(x).
    11.设实数a,b,c,m满足条件：=0，且a≥0,m>0，求证：方程ax²+bx+c=0有一根x₀满足0<x₀<1.
    五、联赛一试水平训练题
    1．不等式|x|³-2x²-4|x|+3<0的解集是_________.
    2．如果实数x, y满足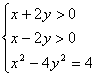：，那么|x|-|y|的最小值是_________.
    3．已知二次函数f(x)=ax²+bx+c的图象经过点（1，1），（3，5），f(0)>0，当函数的最小值取最大值时，a+b²+c³=_________.
    4. 已知f(x)=|1-2x|, x∈[0,1]，方程f(f(f)(x)))=x有_________个实根。
    5．若关于x的方程4x²-4x+m=0在[-1，1]上至少有一个实根，则m取值范围是_________.
    6．若f(x)=x⁴+px³+qx²+x对一切x∈R都有f(x)≥x且f(1)=1，则p+q²=_________.
    7. 对一切x∈R，f(x)=ax²+bx+c(a<b)的值恒为非负实数，则的最小值为_________.
    8．函数f(x)=ax²+bx+c的图象如图，且=b-2ac. 那么b²-4ac_________4. （填>、=、<）
    9．若a<b<c<d，求证：对任意实数t-1, 关于x的方程(x-a)(x-c)+t(x-b)(x-d)=0都有两个不等的实根。
    10．某人解二次方程时作如下练习：他每解完一个方程，如果方程有两个实根，他就给出下一个二次方程：它的常数项等于前一个方程较大的根，x的系数等于较小的根，二次项系数都是1。证明：这种练习不可能无限次继续下去，并求最多能延续的次数。
    11．已知f(x)=ax²+bx+c在[0，1]上满足|f(x)|≤1,试求|a|+|b|+|c|的最大值。
    六、联赛二试水平训练题
    1．设f(x)=ax²+bx+c，a,b,c∈R, a>100，试问满足|f(x)|≤50的整数x最多有几个？
    2．设函数f(x)=ax²+8x+3(a<0)，对于给定的负数a，有一个最大的正数l(a)，使得在整个区间[0，l(a)]上，不等式|f(x)|≤5都成立。求l(a)的最大值及相应a的值。
    3．设x₁,x₂,…,x_n∈[a, a+1]，且设x=, y=, 求f=y-x²的最大值。
    4．F(x)=ax²+bx+c，a,b,c∈R, 且|F(0)|≤1,|F(1)|≤1,|F(-1)|≤1,则对于|x|≤1，求|F(x)|的最大值。
    5．已知f(x)=x²+ax+b，若存在实数m，使得|f(m)|≤,|f(m+1)|≤,求△=a²-4b的最大值和最小值。
    6．设二次函数f(x)=ax²+bx+c (a,b,c∈R, a0)满足下列条件：
    1）当x∈R时，f(x-4)=f(2-x)，且f(x)≥x；
    2）当x∈(0, 2)时，f(x)≤;
    3）f(x)在R上最小值为0。
    求最大的m(m>1)，使得存在t∈R，只要x∈[1, m]就有f(x+t)≤x.
    7.求证：方程3ax²+2bx-(a+b)=0(b0)在(0,1)内至少有一个实根。
    8．设a,b,A,B∈R⁺, a<A, b<B，若n个正数a₁, a₂,…,a_n位于a与A之间，n个正数b₁, b₂,…,b_n位于b与B之间，求证：

    9．设a,b,c为实数，g(x)=ax²+bx+c, |x|≤1，求使下列条件同时满足的a, b, c的值：
    （ⅰ）=381;
    （ⅱ）g(x)_max=444;
    （ⅲ）g(x)_min=364.
    本系列讲座由在人教中数论坛网友“0.1”整理提供，感谢他（她）的分享。
     (责任编辑：admin)

搜索

热门标签:

高中数学精神讲义（二）