|
高中数学竞赛讲义（三） ──函数 一、基础知识 定义1 映射，对于任意两个集合A，B，依对应法则f，若对A中的任意一个元素x，在B中都有唯一一个元素与之对应，则称f: A→B为一个映射。 定义2 单射，若f: A→B是一个映射且对任意x, y∈A, x  y, 都有f(x)f(y)则称之为单射。定义3 满射，若f: A→B是映射且对任意y∈B，都有一个x∈A使得f(x)=y，则称f: A→B是A到B上的满射。 定义4 一一映射，若f: A→B既是单射又是满射，则叫做一一映射，只有一一映射存在逆映射，即从B到A由相反的对应法则f-1构成的映射，记作f-1: A→B。 定义5 函数，映射f: A→B中，若A，B都是非空数集，则这个映射为函数。A称为它的定义域，若x∈A, y∈B，且f(x)=y（即x对应B中的y），则y叫做x的象，x叫y的原象。集合{f(x)|x∈A}叫函数的值域。通常函数由解析式给出，此时函数定义域就是使解析式有意义的未知数的取值范围，如函数y=3  -1的定义域为{x|x≥0,x∈R}.定义6 反函数，若函数f: A→B（通常记作y=f(x)）是一一映射，则它的逆映射f-1: A→B叫原函数的反函数，通常写作y=f-1(x). 这里求反函数的过程是：在解析式y=f(x)中反解x得x=f-1(y)，然后将x, y互换得y=f-1(x)，最后指出反函数的定义域即原函数的值域。例如：函数y=  的反函数是y=1- (x0).定理1 互为反函数的两个函数的图象关于直线y=x对称。 定理2 在定义域上为增（减）函数的函数，其反函数必为增（减）函数。 定义7 函数的性质。 （1）单调性：设函数f(x)在区间I上满足对任意的x1, x2∈I并且x1< x2，总有f(x1)<f(x2)(f(x)>f(x2))，则称f(x)在区间I上是增（减）函数，区间I称为单调增（减）区间。 （2）奇偶性：设函数y=f(x)的定义域为D，且D是关于原点对称的数集，若对于任意的x∈D，都有f(-x)=-f(x)，则称f(x)是奇函数；若对任意的x∈D，都有f(-x)=f(x)，则称f(x)是偶函数。奇函数的图象关于原点对称，偶函数的图象关于y轴对称。 （3）周期性：对于函数f(x)，如果存在一个不为零的常数T，使得当x取定义域内每一个数时，f(x+T)=f(x)总成立，则称f(x)为周期函数，T称为这个函数的周期，如果周期中存在最小的正数T0，则这个正数叫做函数f(x)的最小正周期。 定义8 如果实数a<b，则数集{x|a<x<b, x∈R}叫做开区间，记作（a,b），集合{x|a≤x≤b,x∈R}记作闭区间[a,b]，集合{x|a<x≤b}记作半开半闭区间（a,b]，集合{x|a≤x<b}记作半闭半开区间[a, b)，集合{x|x>a}记作开区间（a, +∞），集合{x|x≤a}记作半开半闭区间（-∞,a]. 定义9 函数的图象，点集{(x,y)|y=f(x), x∈D}称为函数y=f(x)的图象，其中D为f(x)的定义域。通过画图不难得出函数y=f(x)的图象与其他函数图象之间的关系(a,b>0)；（1）向右平移a个单位得到y=f(x-a)的图象；（2）向左平移a个单位得到y=f(x+a)的图象；（3）向下平移b个单位得到y=f(x)-b的图象；（4）与函数y=f(-x)的图象关于y轴对称；（5）与函数y=-f(-x)的图象关于原点成中心对称；（6）与函数y=f-1(x)的图象关于直线y=x对称；（7）与函数y=-f(x)的图象关于x轴对称。 定理3 复合函数y=f[g(x)]的单调性，记住四个字：“同增异减”。例如y=  , u=2-x在（-∞,2）上是减函数，y= 在（0，+∞）上是减函数，所以y=在（-∞,2）上是增函数。注：复合函数单调性的判断方法为同增异减。这里不做严格论证，求导之后是显然的。 二、方法与例题 1．数形结合法。 例1 求方程|x-1|= 的正根的个数.【解】 分别画出y=|x-1|和y= 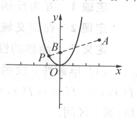的图象，由图象可知两者有唯一交点，所以方程有一个正根。例2 求函数f(x)=  的最大值。 【解】 f(x)=  ，记点P(x, x?2)，A（3，2），B（0，1），则f(x)表示动点P到点A和B距离的差。 因为|PA|-|PA|≤|AB|=  ,当且仅当P为AB延长线与抛物线y=x2的交点时等号成立。所以f(x)max=  2.函数性质的应用。 例3 设x, y∈R，且满足  ，求x+y.【解】 设f(t)=t3+1997t，先证f(t)在（-∞，+∞）上递增。事实上，若a<b，则f(b)-f(a)=b3-a3+1997(b-a)=(b-a)(b2+ba+a2+1997)>0，所以f(t)递增。 由题设f(x-1)=-1=f(1-y)，所以x-1=1-y，所以x+y=2. 例4 奇函数f(x)在定义域（-1，1）内是减函数，又f(1-a)+f(1-a2)<0，求a的取值范围。 【解】 因为f(x) 是奇函数，所以f(1-a2)=-f(a2-1)，由题设f(1-a)<f(a2-1)。 又f(x)在定义域（-1，1）上递减，所以-1<1-a<a2-1<1，解得0<a<1。 例5 设f(x)是定义在（-∞，+∞）上以2为周期的函数，对k∈Z, 用Ik表示区间(2k-1, 2k+1]，已知当x∈I0时，f(x)=x2，求f(x)在Ik上的解析式。 【解】 设x∈Ik，则2k-1<x≤2k+1， 所以f(x-2k)=(x-2k)2. 又因为f(x)是以2为周期的函数， 所以当x∈Ik时，f(x)=f(x-2k)=(x-2k)2. 例6 解方程：(3x-1)(  )+(2x-3)( +1)=0.【解】 令m=3x-1, n=2x-3，方程化为 m(  +1)+n( +1)=0. ①若m=0，则由①得n=0，但m, n不同时为0，所以m 0, n0.ⅰ)若m>0，则由①得n<0，设f(t)=t(  +1),则f(t)在（0，+∞）上是增函数。又f(m)=f(-n)，所以m=-n，所以3x-1+2x-3=0，所以x= ⅱ)若m<0，且n>0。同理有m+n=0,x=  ,但与m<0矛盾。综上，方程有唯一实数解x= 3.配方法。 例7 求函数y=x+  的值域。【解】 y=x+ = [2x+1+2+1]-1= (+1)-1≥-1=-.当x=- 时，y取最小值-，所以函数值域是[-，+∞）。4．换元法。 例8 求函数y=(  + +2)( +1),x∈[0,1]的值域。【解】令 +=u，因为x∈[0,1]，所以2≤u2=2+2≤4,所以 ≤u≤2,所以 ≤ ≤2，1≤ ≤2，所以y=,u2∈[+2，8]。所以该函数值域为[2+ ，8]。5．判别式法。 例9 求函数y=  的值域。【解】由函数解析式得(y-1)x2+3(y+1)x+4y-4=0. ① 当y 1时，①式是关于x的方程有实根。所以△=9(y+1)2-16(y-1)2≥0，解得  ≤y≤1.又当y=1时，存在x=0使解析式成立， 所以函数值域为[ ，7]。6．关于反函数。 例10 若函数y=f(x)定义域、值域均为R，且存在反函数。若f(x)在(-∞,+ ∞)上递增，求证：y=f-1(x)在(-∞,+ ∞)上也是增函数。 【证明】设x1<x2, 且y1=f-1(x1), y2=f-1(x2)，则x1=f(y1), x2=f(y2)，若y1≥y2，则因为f(x)在(-∞,+ ∞)上递增，所以x1≥x2与假设矛盾，所以y1<y2。 即y=f-1(x)在(-∞,+ ∞)递增。 例11 设函数f(x)=  ，解方程：f(x)=f-1(x).【解】 首先f(x)定义域为（-∞，-  ）∪[- ，+∞）；其次，设x1, x2是定义域内变量，且x1<x2<-;  = >0,所以f(x)在（-∞，- ）上递增，同理f(x)在[-，+∞）上递增。在方程f(x)=f-1(x)中，记f(x)=f-1(x)=y，则y≥0，又由f-1(x)=y得f(y)=x，所以x≥0,所以x,y∈[- ，+∞）.若x y，设x<y，则f(x)=y<f(y)=x，矛盾。同理若x>y也可得出矛盾。所以x=y. 即f(x)=x，化简得3x5+2x4-4x-1=0, 即(x-1)(3x4+5x3+5x2+5x+1)=0, 因为x≥0，所以3x4+5x3+5x2+5x+1>0，所以x=1. 三、基础训练题 1．已知X={-1, 0, 1}, Y={-2, -1, 0, 1, 2}，映射f：X→Y满足：对任意的x∈X，它在Y中的象f(x)使得x+f(x)为偶数，这样的映射有_______个。 2．给定A={1，2，3}，B={-1，0，1}和映射f：X→Y，若f为单射，则f有_______个；若f为满射，则f有_______个；满足f[f(x)] =f(x)的映射有_______个。 3．若直线y=k(x-2)与函数y=x2+2x图象相交于点（-1，-1），则图象与直线一共有_______个交点。 4．函数y=f(x)的值域为[  ]，则函数g(x)=f(x)+ 的值域为_______。5．已知f(x)=  ，则函数g(x)=f[f(x)]的值域为_______。6．已知f(x)=|x+a|，当x≥3时f(x)为增函数，则a的取值范围是_______。 7．设y=f(x)在定义域（ ，2）内是增函数，则y=f(x2-1)的单调递减区间为_______。8．若函数y=  (x)存在反函数y=-1(x)，则y=-1(x)的图象与y=-(-x)的图象关于直线_______对称。9．函数f(x)满足  =1- ，则f()=_______。10. 函数y=  , x∈(1, +∞)的反函数是_______。11．求下列函数的值域：（1）y=  ; (2)y= ; (3)y=x+2 ; (4) y= 12. 已知  定义在R上，对任意x∈R, f(x)=f(x+2)，且f(x)是偶函数，又当x∈[2,3]时，f(x)=x，则当x∈[-2,0]时，求f(x)的解析式。四、高考水平训练题 1．已知a∈  , f(x)定义域是（0,1]，则g(x)=f(x+a)+f(x-a)+f(x)的定义域为_______。2．设0≤a<1时，f(x)=(a-1)x2-6ax+a+1恒为正值。则f(x)定义域为_______。 3．映射f: {a, b, c, d}→{1，2，3}满足10<f(a)·f(b)·f(c)·f(d)<20，这样的映射f有_______个。 4．设函数y=f(x)(x∈R)的值域为R，且为增函数，若方程f(x)=x解集为P，f[f(x)]=x解集为Q，则P，Q的关系为：P_______Q（填=、  、 ）。5．下列函数是否为奇函数：（1）f(x)=(x-1)  ；（2）g(x)=|2x+1|-|2x-1| ; (3) (x)= ；（4）y= 6. 设函数y=f(x)(x∈R且x 0)，对任意非零实数x1, x2满足f(x1x2)=f(x1)+f(x2)，又f(x)在（0，+∞）是增函数，则不等式f(x)+f(x-)≤0的解集为_______。7．函数f(x)=  ，其中P，M为R的两个非空子集，又规定f(P)={y|y=f(x), x∈P}, f(M)={y|y=f(x), x∈M}，给出如下判断：①若P∩M= ，则f(P) ∩f(M)=；②若P∩M，则f(P) ∩f(M)；③若P∪M=R, 则f(P) ∪f(M)=R；④若P∪MR，则f(P) ∪f(M)R. 其中正确的判断是_______。8．函数y=f(x+1)的反函数是y=f-1(x+1)，并且f(1)=3997，则f(1998)= _______。 9．已知y=f(x)是定义域为[-6，6]的奇函数，且当x∈[0，3]时是一次函数，当x∈[3，6]时是二次函数，又f(6)=2，当x∈[3，6]时，f(x)≤f(5)=3。求f(x)的解析式。 10．设a>0，函数f(x)定义域为R，且f(x+a)=  ，求证：f(x)为周期函数。11．设关于x的方程2x2-tx-2=0的两根为α，β（α<β），已知函数f(x)= 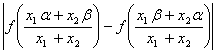 ,（1）求f(α)、f(β)；（2）求证：f(x)在[α，β]上是增函数；（3）对任意正数x1, x2，求证： <2|α-β|.五、联赛一试水平训练题 1．奇函数f(x)存在函数f-1(x)，若把y=f(x)的图象向上平移3个单位，然后向右平移2个单位后，再关于直线y=-x对称，得到的曲线所对应的函数是________. 2．若a>0，a 1,F(x)是奇函数，则G(x)=F(x) 是________（奇偶性）.3．若  =x，则下列等式中正确的有________.①F(-2-x)=-2-F(x)；②F(-x)= ；③F(x-1)=F(x)；④F(F(x))=-x.4.设函数f：R→R满足f(0)=1，且对任意x,y∈R，都有f(xy+1)=f(x)f(y)-f(y)-x+2，则f(x)=________. 5．已知f(x)是定义在R上的函数，f(1)=1，且对任意x∈R都有f(x+5)≥f(x)+5, f(x+1) ≤f(x)+1。若g(x)=f(x)+1-x，则g(2002)= ________. 6. 函数f(x)=  的单调递增区间是________.7. 函数f(x)=  的奇偶性是：________奇函数，________偶函数（填是，非）。8. 函数y=x+  的值域为________.9．设f(x)=  ,对任意的a∈R，记V(a)=max{f(x)-ax|x∈[1, 3]}-min{f(x)-ax|x∈[1, 3]}，试求V(a)的最小值。 10．解方程组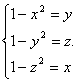：  （在实数范围内）11．设k∈N+, f: N+→N+满足：（1）f(x)严格递增；（2）对任意n∈N+, 有f[f(n)]=kn，求证：对任意n∈N+, 都有  n≤f(n)≤ 六、联赛二试水平训练题 1．求证：恰有一个定义在所有非零实数上的函数f，满足：（1）对任意x≠0, f(x)=x·f  ；（2）对所有的x≠-y且xy≠0，有f(x)+f(y)=1+f(x+y).2.设f(x)对一切x>0有定义，且满足：（ⅰ）f(x)在（0，+∞）是增函数；(ⅱ)任意x>0, f(x)f  =1，试求f(1).3. f:[0,1]→R满足：（1）任意x∈[0, 1], f(x)≥0；（2）f(1)=1；（3）当x, y, x+y∈[0, 1]时，f(x)+f(y)≤f(x+y)，试求最小常数c，对满足（1），（2），（3）的函数f(x)都有f(x)≤cx. 4. 试求f(x,y)=6(x2+y2)(x+y)-4(x2+xy+y2)-3(x+y)+5(x>0, y>0)的最小值。 5．对给定的正数p,q∈(0, 1)，有p+q>1≥p2+q2，试求f(x)=(1-x)  + 在[1-q,p]上的最大值。6．已知f: (0,1)→R且f(x)=  .当x∈  时，试求f(x)的最大值。7．函数f(x)定义在整数集上，且满足f(n)=  ，求f(100)的值。8．函数y=f(x)定义在整个实轴上，它的图象在围绕坐标原点旋转角  后不变。（1）求证：方程f(x)=x恰有一个解；（2）试给出一个具有上述性质的函数。9．设Q+是正有理数的集合，试构造一个函数f: Q+→Q+，满足这样的条件：f(xf(y))=  x, y∈Q+.本系列讲座由在人教中数论坛网友“0.1”整理提供，感谢他（她）的分享。 (责任编辑：admin) |