|
高中数学竞赛讲义（四） ──几个初等函数的性质 一、基础知识 1．指数函数及其性质：形如y=ax(a>0, a  1)的函数叫做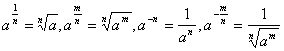指数函数，其定义域为R，值域为（0，+∞），当0<a<1时，y=ax是减函数，当a>1时，y=ax为增函数，它的图象恒过定点（0，1）。2．分数指数幂：  。3．对数函数及其性质：形如y=logax(a>0, a 1)的函数叫做对数函数，其定义域为（0，+∞），值域为R，图象过定点（1，0）。当0<a<1，y=logax为减函数，当a>1时，y=logax为增函数。4．对数的性质（M>0, N>0）； 1）ax=M  x=logaM(a>0, a1)；2）loga(MN)= loga M+ loga N； 3）loga（  ）= loga M- loga N；4）loga Mn=n loga M；，5）loga  = loga M；6）aloga M=M; 7) loga b= (a,b,c>0, a, c1).5. 函数y=x+  （a>0）的单调递增区间是 和 ，单调递减区间为 和 。（请读者自己用定义证明）6．连续函数的性质：若a<b, f(x)在[a, b]上连续，且f(a)·f(b)<0，则f(x)=0在（a,b）上至少有一个实根。 二、方法与例题 1．构造函数解题。 例1 已知a, b, c∈(-1, 1)，求证：ab+bc+ca+1>0. 【证明】 设f(x)=(b+c)x+bc+1 (x∈(-1, 1))，则f(x)是关于x的一次函数。 所以要证原不等式成立，只需证f(-1)>0且f(1)>0（因为-1<a<1）. 因为f(-1)=-(b+c)+bc+1=(1-b)(1-c)>0， f(1)=b+c+bc+a=(1+b)(1+c)>0， 所以f(a)>0，即ab+bc+ca+1>0. 例2 （柯西不等式）若a1, a2,…,an是不全为0的实数，b1, b2,…,bn∈R，则（  ）·（ ）≥( )2，等号当且仅当存在 R，使ai= , i=1, 2, …, n时成立。【证明】 令f(x)= （ ）x2-2()x+= ,因为 >0，且对任意x∈R, f(x)≥0，所以△=4( )-4（）()≤0.展开得（ ）()≥()2。等号成立等价于f(x)=0有实根，即存在  ，使ai=, i=1, 2, …, n。例3 设x, y∈R+, x+y=c, c为常数且c∈(0, 2]，求u=  的最小值。【解】u= =xy+ ≥xy+ +2· =xy+ +2.令xy=t，则0<t=xy≤  ,设f(t)=t+ ,0<t≤ 因为0<c≤2，所以0<  ≤1，所以f(t)在 上单调递减。所以f(t)min=f( )=+ ，所以u≥++2.当x=y=  时，等号成立. 所以u的最小值为++2.2．指数和对数的运算技巧。 例4 设p, q∈R+且满足log9p= log12q= log16(p+q)，求  的值。【解】 令log9p= log12q= log16(p+q)=t，则p=9 t , q=12 t , p+q=16t， 所以9 t +12 t =16 t，即1+  记x=  ，则1+x=x2，解得 又 >0，所以= 例5 对于正整数a, b, c(a≤b≤c)和实数x, y, z, w，若ax=by=cz=70w，且  ，求证：a+b=c.【证明】 由ax=by=cz=70w取常用对数得xlga=ylgb=zlgc=wlg70. 所以  lga= lg70, lgb= lg70, lgc= lg70，相加得 (lga+lgb+lgc)= lg70，由题设，所以lga+lgb+lgc=lg70，所以lgabc=lg70. 所以abc=70=2×5×7. 若a=1，则因为xlga=wlg70，所以w=0与题设矛盾，所以a>1. 又a≤b≤c，且a, b, c为70的正约数，所以只有a=2, b=5, c=7. 所以a+b=c. 例6 已知x 1, ac1, a1, c1. 且logax+logcx=2logbx，求证c2=(ac)logab.【证明】 由题设logax+logcx=2logbx，化为以a为底的对数，得  ，因为ac>0, ac 1，所以logab=logacc2，所以c2=(ac)logab.注：指数与对数式互化，取对数，换元，换底公式往往是解题的桥梁。 3．指数与对数方程的解法。 解此类方程的主要思想是通过指对数的运算和换元等进行化简求解。值得注意的是函数单调性的应用和未知数范围的讨论。 例7 解方程：3x+4 x +5 x =6 x. 【解】 方程可化为  =1。设f(x)= , 则f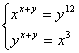(x)在(-∞,+∞)上是减函数，因为f(3)=1，所以方程只有一个解x=3.例8 解方程组：  （其中x, y∈R+）.【解】 两边取对数，则原方程组可化为  ①②把①代入②得(x+y)2lgx=36lgx，所以[(x+y)2-36]lgx=0. 由lgx=0得x=1，由(x+y)2-36=0(x, y∈R+)得x+y=6， 代入①得lgx=2lgy，即x=y2，所以y2+y-6=0. 又y>0，所以y=2, x=4. 所以方程组的解为  .例9 已知a>0, a 1，试求使方程loga(x-ak)=loga2(x2-a2)有解的k的取值范围。【解】由对数性质知，原方程的解x应满足 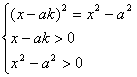 .①②③若①、②同时成立，则③必成立， 故只需解 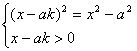 . 由①可得2kx=a(1+k2)， ④ 当k=0时，④无解；当k 0时，④的解是x= ，代入②得 >k.若k<0，则k2>1，所以k<-1；若k>0，则k2<1，所以0<k<1. 综上，当k∈(-∞,-1) ∪(0, 1)时，原方程有解。 三、基础训练题 1．命题p: “(log23)x-(log53)x≥(log23)-y-(log53)-y”是命题q:“x+y≥0”的_________条件。 2．如果x1是方程x+lgx=27的根，x2是方程x+10x=27的根，则x1+x2=_________. 3．已知f(x)是定义在R上的增函数，点A（-1，1），B（1，3）在它的图象上，y=f-1(x)是它的反函数，则不等式|f-1(log2x)|<1的解集为_________。 4．若log2a 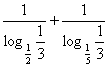 <0，则a 取值范围是_________。5．命题p: 函数y=log2  在[2，+∞）上是增函数；命题q: 函数y=log2(ax2-4x+1)的值域为R，则p是q的_________条件。6．若0<b<1, a>0且a 1，比较大小：|loga(1-b)|_________|loga(1+b).7．已知f(x)=2+log3x, x∈[1, 3]，则函数y=[f(x)]2+f(x2)的值域为_________。 8．若x=  ，则与x最接近的整数是_________。9．函数  的单调递增区间是_________。10．函数f(x)=  的值域为_________。11．设f(x)=lg[1+2x+3 x +…+(n-1) x +n x·a]，其中n为给定正整数, n≥2, a∈R.若f(x)在x∈(-∞,1]时有意义，求a的取值范围。 12．当a为何值时，方程  =2有一解，二解，无解？四、高考水平训练题 1．函数f(x)= 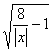 +lg(x2-1)的定义域是_________.2．已知不等式x2-logmx<0在x∈  时恒成立，则m的取值范围是_________.3．若x∈{x|log2x=2-x}，则x2, x, 1从大到小排列是_________. 4. 若f(x)=ln  ，则使f(a)+f(b)= _________.5. 命题p: 函数y=log2 在[2，+∞）上是增函数；命题q：函数y=log2(ax2-4x+1)的值域为R，则p是q的_________条件.6．若0<b<1, a>0且a 1，比较大小：|loga(1-b)| _________|loga(1+b)|.7．已知f(x)=2+log3x, x∈[1, 3]，则函数y=[f(x)]2+f(x2)的值域为_________. 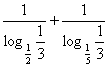8．若x= ，则与x最接近的整数是_________.9．函数y=  的单调递增区间是_________.10．函数f(x)= 的值域为_________.11．设f(x)=lg[1+2x+3 x +…+(n-1) x +n x·a]，其中n为给定正整数，n≥2,a∈R。若f(x) 在x∈(-∞,1]时有意义，求a的取值范围。 12．当a为何值时，方程 =2有一解，二解，无解？四、高考水平训练题 1．函数f(x)= 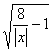+lg(x2-1)的定义域是__________.2．已知不等式x2-logmx<0在x∈ 时恒成立，则m的取值范围是 ________.3．若x∈{x|log2x=2-x}，则x2, x, 1从大到小排列是________. 4．若f(x)=ln ，则使f(a)+f(b)=成立的a, b的取值范围是________.5．已知an=logn(n+1)，设  ，其中p, q为整数，且(p ,q)=1，则p·q的值为_________.6．已知x>10, y>10, xy=1000，则(lgx)·(lgy)的取值范围是________. 7．若方程lg(kx)=2lg(x+1)只有一个实数解，则实数k的取值范围是________. 8．函数f(x)=  的定义域为R，若关于x的方程f?2(x)+bf(x)+c=0有7个不同的实数解，则b, c应满足的充要条件是________.（1）b<0且c>0；（2）b>0且c<0；（3）b<0且c=0；（4）b≥0且c=0。 9．已知f(x)=  x, F(x)=f(x+t)-f(x-t)(t0)，则F(x)是________函数（填奇偶性）.10．已知f(x)=lg  ，若 =1， =2，其中|a|<1, |b|<1，则f(a)+f(b)=________.11．设a∈R，试讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实数解的个数。 12．设f(x)=|lgx|，实数a, b满足0<a<b, f(a)=f(b)=2f  ，求证：（1）a4+2a2-4a+1=0, b4-4b3+2b2+1=0；（2）3<b<4. 13．设a>0且a 1, f(x)=loga(x+ )(x≥1)，（1）求f(x)的反函数f-1(x)；（2）若f-1(n)< (n∈N+)，求a的取值范围。五、联赛一试水平训练题 1．如果log2[log  (log2x)]= log3[log (log3x)]= log5[log (log5z)]=0，那么将x, y, z从小到大排列为___________.2．设对任意实数x0> x1> x2> x3>0，都有log  1993+ log 1993+ log 1993> klog 1993恒成立，则k的最大值为___________.3．实数x, y满足4x2-5xy+4y2=5，设S=x2+y2，则  的值为___________.4．已知0<b<1, 00<α<450，则以下三个数：x=(sinα)logbsina, y=(cosα) logbsina, z=(sinα) logbsina从小到大排列为___________. 5．用[x]表示不超过x的最大整数，则方程lg2x-[lgx]-2=0的实根个数是___________. 6．设a=lgz+lg[x(yz)-1+1], b=lgx-1+lg[xyz+1], c=lgy+lg[(xyz)-1+1]，记a, b, c中的最大数为M，则M的最小值为___________. 7．若f(x)(x∈R)是周期为2的偶函数，当x∈[0,1]时，f(x)=  ，则 ， 由小到大排列为___________.8．不等式  +2>0的解集为___________.9．已知a>1, b>1，且lg(a+b)=lga+lgb，求lg(a-1)+lg(b-1). 10．（1）试画出由方程  所确定的函数y=f(x)图象。（2）若函数y=ax+  与y=f(x)的图象恰有一个公共点，求a的取值范围。11．对于任意n∈N+(n>1)，试证明：[  ]+[ ]+…+[ ]=[log2n]+[log3n]+…+[lognn]。六、联赛二试水平训练题 1．设x, y, z∈R+且x+y+z=1，求u=  的最小值。2．当a为何值时，不等式log  ·log5(x2+ax+6)+loga3≥0有且只有一个解（a>1且a1）。3．f(x)是定义在（1，+∞）上且在（1，+∞）中取值的函数，满足条件；对于任何x, y>1及u, v>0, f(xuyv)≤[f(x)]  [f(y)] ①都成立，试确定所有这样的函数f(x).4. 求所有函数f：R→R，使得xf(x)-yf(x)=(x-y)f(x+y)①成立。 5．设m≥14是一个整数，函数f：N→N定义如下： f(n)=  ,求出所有的m,使得f(1995)=1995. 6．求定义在有理数集上且满足下列条件的所有函数f: f(x+y)=f(x)+f(y)+f(x)·f(y), x, y∈Q. 7．是否存在函数f(n)，将自然数集N映为自身，且对每个n>1, f(n)=f(f(n-1))+f(f(n+1))都成立。 8．设p, q是任意自然数，求证：存在这样的f(x) ∈Z(x)（表示整系数多项式集合），使对x轴上的某个长为  的开区间中的每一个数x, 有 9．设α，β为实数，求所有f: R+→R，使得对任意的x,y∈R+, f(x)f(y)=y2·f  成立。本系列讲座由在人教中数论坛网友“0.1”整理提供，感谢他（她）的分享。 (责任编辑：admin) |