|
不定方程 所谓不定方程，是指未知数的个数多于方程个数，且未知数受到某些（如要求是有理数、整数或正整数等等）的方程或方程组。不定方程也称为丢番图方程，是数论的重要分支学科，也是历史上最活跃的数学领域之一。不定方程的内容十分丰富，与代数数论、几何数论、集合数论等等都有较为密切的联系。不定方程的重要性在数学竞赛中也得到了充分的体现，每年世界各地的数学竞赛吉，不定方程都占有一席之地；另外它也是培养学生思维能力的好材料，数学竞赛中的不定方程问题，不仅要求学生对初等数论的一般理论、方法有一定的了解，而且更需要讲究思想、方法与技巧，创造性的解决问题。在本节我们来看一看不定方程的基础性的题目。 基础知识 1．不定方程问题的常见类型： （1）求不定方程的解； （2）判定不定方程是否有解； （3）判定不定方程的解的个数（有限个还是无限个）。 2．解不定方程问题常用的解法： （1）代数恒等变形：如因式分解、配方、换元等； （2）不等式估算法：利用不等式等方法，确定出方程中某些变量的范围，进而求解； （3）同余法：对等式两边取特殊的模（如奇偶分析），缩小变量的范围或性质，得出不定方程的整数解或判定其无解； （4）构造法：构造出符合要求的特解，或构造一个求解的递推式，证明方程有无穷多解； （5）无穷递推法。 以下给出几个关于特殊方程的求解定理： （一）二元一次不定方程（组） 定义1.形如  (  不同时为零)的方程称为二元一次不定方程。定理1.方程 有解的充要是 ；定理2.若  ，且 为的一个解，则方程的一切解都可以表示成  为任意整数)。定理3.  元一次不定方程 ，( )有解的充要条件是 .方法与技巧： 1．解二元一次不定方程通常先判定方程有无解。若有解，可先求 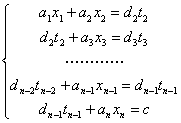一个特解，从而写出通解。当不定方程系数不大时，有时可以通过观察法求得其解，即引入变量，逐渐减小系数，直到容易得其特解为止；2．解 元一次不定方程 时，可先顺次求出 ，……，  .若   ，则方程无解；若|，则方程有解，作方程组： 求出最后一个方程的一切解，然后把 的每一个值代入倒数第二个方程，求出它的一切解，这样下去即可得方程的一切解。3．  个元一次不定方程组成的方程组，其中 ，可以消去 个未知数，从而消去了个不定方程，将方程组转化为一个 元的一次不定方程。（二）高次不定方程（组）及其解法 1．因式分解法：对方程的一边进行因式分解，另一边作质因式分解，然后对比两边，转而求解若干个方程组； 2．同余法：如果不定方程  有整数解，则对于任意 ，其整数解 满足 ，利用这一条件，同余可以作为探究不定方程整数解的一块试金石；3．不等式估计法：利用不等式工具确定不定方程中某些字母的范围，再分别求解； 4．无限递降法：若关于正整数 的命题 对某些正整数成立，设 是使成立的最小正整数，可以推出：存在 ，使得 成立，适合证明不定方程无正整数解。方法与技巧： 1．因式分解法是不定方程中最基本的方法，其理论基础是整数的唯一分解定理，分解法作为解题的一种手段，没有因定的程序可循，应具体的例子中才能有深刻地体会； 2．同余法主要用于证明方程无解或导出有解的必要条件，为进一步求解或求证作准备。同余的关键是选择适当的模，它需要经过多次尝试； 3．不等式估计法主要针对方程有整数解，则必然有实数解，当方程的实数解为一个有界集，则着眼于一个有限范围内的整数解至多有有限个，逐一检验，求出全部解；若方程的实数解是无界的，则着眼于整数，利用整数的各种性质产生适用的不等式； 4．无限递降法论证的核心是设法构造出方程的新解，使得它比已选择的解“严格地小”，由此产生矛盾。 （三）特殊的不定方程 1．利用分解法求不定方程 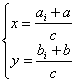 整数解的基本思路：将  转化为 后，若 可分解为 ，则解的一般形式为 ，再取舍得其整数解；2．定义2：形如  的方程叫做勾股数方程，这里 为正整数。对于方程 ，如果 ，则 ，从而只需讨论 的情形，此时易知两两互素，这种两两互素的正整数组叫方程的本原解。定理3.勾股数方程 满足条件 的一切解可表示为： ，其中 且为一奇一偶。推论：勾股数方程 的全部正整数解（ 的顺序不加区别）可表示为： 其中 是互质的奇偶性不同的一对正整数， 是一个整数。勾股数不定方程 的整数解的问题主要依据定理来解决。3．定义3.方程  且不是平方数)是 的一种特殊情况，称为沛尔(Pell)方程。这种二元二次方程比较复杂，它们本质上归结为双曲线方程 的研究，其中 都是整数， 且非平方数，而 。它主要用于证明问题有无数多个整数解。对于具体的可用尝试法求出一组成正整数解。如果上述pell方程有正整数解 ，则称使 的最小的正整数解 为它的最小解。定理4.Pell方程 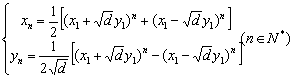 且不是平方数)必有正整数解，且若设它的最小解为，则它的全部解可以表示成： .上面的公式也可以写成以下几种形式： （1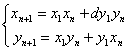）  ；（2） ；（3） .定理5.Pell方程 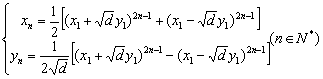 且不是平方数)要么无正整数解，要么有无穷多组正整数解，且在后一种情况下，设它的最小解为，则它的全部解可以表示为 定理6. （费尔马（Fermat）大定理）方程  为整数)无正整数解。费尔马（Fermat）大定理的证明一直以来是数学界的难题，但是在1994年6月，美国普林斯顿大学的数学教授A.Wiles完全解决了这一难题。至此，这一困扰了人们四百多年的数学难题终于露出了庐山真面目，脱去了其神秘面纱。 典例分析 例1．求不定方程  的整数解。解：先求  的一组特解，为此对37，107运用辗转相除法： ， ，  将上述过程回填，得：   由此可知，  是方程的一组特解，于是 ， 是方程 的一组特解，因此原方程的一 切整数解为： 。例2．求不定方程  的所有正整数解。解：用原方程中的最小系数7去除方程的各项，并移项得：  因为 是整数，故 也一定是整数，于是有 ，再用5去除比式的两边，得 ，令 为整数，由此得 。经观察得  是最后一个方程的一组解，依次回代，可求得原方程的一组特解： ，所以原方程的一切整数解为： 。例3．求不定方程  的正整数解。解：显然此方程有整数解。先确定系数最大的未知数  的取值范围，因为 的最小值为1，所以 。当  时，原方程变形为 ，即 ，由上式知 是偶数且 故方程组有5组正整数解，分别为 ， ， ， ， ；当  时，原方程变形为 ，即 ，故方程有3组正整数解，分别为： ， ， ；当  时，原方程变形为 ，即 ，故方程有2组正整数解，分别为： ， ；当  时，原方程变形为 ，即 ，故方程只有一组正整数解，为 。故原方程有11组正整数解（如下表）：
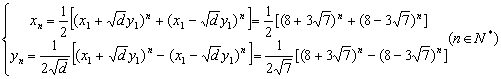例4．求出方程  的所有正整数解。解：先求最小解  。令 当  时， ；当 时， ；当 时， 。所以的最小解为 ，于是： 例5．在直角坐标平面上，以（199，0）为圆心，以199为半径的圆周上的整点的个数为多少个？ 解：设  为圆 上任一整点，则其方程为： ；显然  为方程的4组解。但当  时， （因为199是质数），此时， 是一组勾股数，故199可表示为两个正整数的平方和，即 。因为  ，可设 ，则  这与199为  型的质数矛盾！因而圆O上只有四个整点  。例6．求所有满足  的正整数三元组 。解：两边取  ，得 ，所以 是偶数，再 得 ，所以也是偶数。此时令 于是，由 可知：  ；由唯一分解定理：  ， ，从而  注意到17是奇数，所以要使 成立，一定有 。于是  。当  时，在的两边取 ，得 ，这显然是不成立的，所以 ，从而 。故方程 只有唯一的一组解（2，2，2）。例7．  是一个给定的整数，当为何值时，的方程 有正整数解？在有正整数解时，求解该不定方程。解；若有质数  ， ，则 ，从而 ，矛盾！所以 。因此  当且仅当 。因为  ，显然，所以当且仅当 。（*）（1）若 时， ，所以 或 ， 或 ；（2）类似地，若  ，则 ，所以或， 或 ；（3）由于条件（*），不妨设  ；若  ，则 ，所以 ；若  ，则因为 ，所以存在 ，使得： ，所以  ， 。因为  ，所以必有 。所以  ，故 所以  ，所以或当 时， ；当 时，，对应的为1或2。由条件（*）知  以及 也是原方程的解，对应的整数为14或9。综上，当  时原方程有整数解，它们分别是：（3，1），（5，2）；（2，1），（5，3），（2，2）；（1，2），（3，5）；（1，3），（2，5）。例8．求证：边长为整数的直角三角形的面积不可能是完全平方数。 证明：假设结论不成立，在所有的面积为平方数勾股三角形中选取一个面积最小的，设其边长为  ，则 是平方数，则必有 。因为  ，故存在整数 中一奇一偶， ，使得（不妨设是偶数） 。由于  是完全平方数，而知 两两互素，故它们是平方数，即  ，所以  即 因为  是奇数，易知 ，于是 与 中有一个是 ，另一个是 ，而 ；另一方面，  得  所以，以  为边的三角形都是直角三角形，其面积等于 是平方数，但是  ，于是构造出了一个面积更小的勾股三角形，矛盾！(责任编辑：admin) |