初等数论中的几个重要定理
基础知识
定义(欧拉(Euler)函数)一组数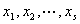 称为是模 称为是模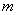 的既约剩余系,如果对任意的 的既约剩余系,如果对任意的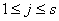 , ,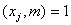 且对于任意的 且对于任意的 ,若 ,若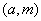 =1,则有且仅有一个 =1,则有且仅有一个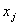 是 是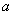 对模 对模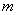 的剩余,即 的剩余,即 。并定义 。并定义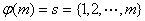 中和 中和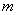 互质的数的个数, 互质的数的个数, 称为欧拉(Euler)函数。 称为欧拉(Euler)函数。
这是数论中的非常重要的一个函数,显然 ,而对于 ,而对于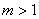 , , 就是1,2,…, 就是1,2,…, 中与 中与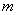 互素的数的个数,比如说 互素的数的个数,比如说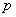 是素数,则有 是素数,则有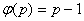 。 。
引理: ;可用容斥定理来证(证明略)。 ;可用容斥定理来证(证明略)。
定理1:(欧拉(Euler)定理)设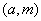 =1,则 =1,则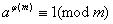 。 。
分析与解答:要证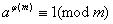 ,我们得设法找出 ,我们得设法找出 个 个 相乘,由 相乘,由 个数我们想到 个数我们想到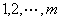 中与 中与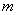 互质的 互质的 的个数: 的个数: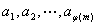 ,由于 ,由于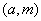 =1,从而 =1,从而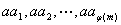 也是与 也是与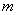 互质的 互质的 个数,且两两余数不一样,故 个数,且两两余数不一样,故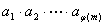 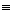 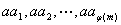 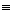 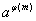 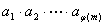 ( (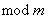 ),而( ),而(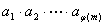 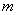 )=1,故 )=1,故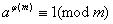 。 。
证明:取模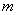 的一个既约剩余系 的一个既约剩余系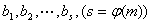 ,考虑 ,考虑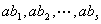 ,由于 ,由于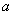 与 与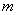 互质,故 互质,故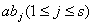 仍与 仍与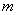 互质,且有 互质,且有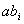 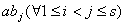 ,于是对每个 ,于是对每个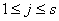 都能找到唯一的一个 都能找到唯一的一个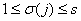 ,使得 ,使得 ,这种对应关系 ,这种对应关系 是一一的,从而 是一一的,从而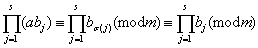 , , 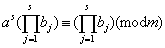 。 。
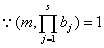 , ,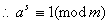 ,故 ,故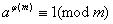 。证毕。 。证毕。
这是数论证明题中常用的一种方法,使用一组剩余系,然后乘一个数组组成另外一组剩余系来解决问题。
定理2:(费尔马(Fermat)小定理)对于质数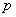 及任意整数 及任意整数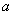 有 有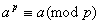 。 。
设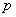 为质数,若 为质数,若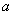 是 是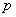 的倍数,则 的倍数,则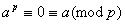 。若 。若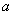 不是 不是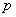 的倍数,则 的倍数,则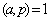 由引理及欧拉定理得 由引理及欧拉定理得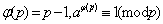 , ,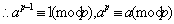 ,由此即得。 ,由此即得。
定理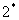 推论:设 推论:设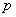 为质数, 为质数,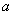 是与 是与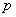 互质的任一整数,则 互质的任一整数,则 。 。
定理3:(威尔逊(Wilson)定理)设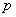 为质数,则 为质数,则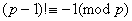 。 。
分析与解答:受欧拉定理的影响,我们也找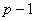 个数,然后来对应乘法。 个数,然后来对应乘法。
证明:对于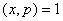 ,在 ,在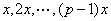 中,必然有一个数除以 中,必然有一个数除以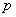 余1,这是因为 余1,这是因为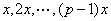 则好是 则好是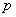 的一个剩余系去0。 的一个剩余系去0。
从而对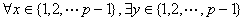 ,使得 ,使得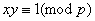 ; ;
若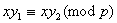 , ,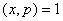 ,则 ,则 , ,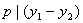 ,故对于 ,故对于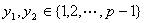 ,有 ,有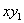  。即对于不同的 。即对于不同的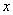 对应于不同的 对应于不同的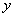 ,即 ,即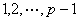 中数可两两配对,其积除以 中数可两两配对,其积除以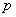 余1,然后有 余1,然后有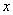 ,使 ,使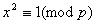 ,即与它自己配对,这时 ,即与它自己配对,这时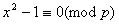 , , , , 或 或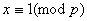 , ,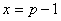 或 或 。 。
除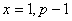 外,别的数可两两配对,积除以 外,别的数可两两配对,积除以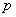 余1。故 余1。故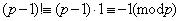 。 。
定义:设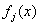 为整系数多项式( 为整系数多项式(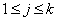 ),我们把含有 ),我们把含有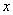 的一组同余式 的一组同余式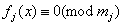 ( (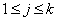 )称为同余方组程。特别地,,当 )称为同余方组程。特别地,,当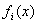 均为 均为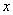 的一次整系数多项式时,该同余方程组称为一次同余方程组.若整数 的一次整系数多项式时,该同余方程组称为一次同余方程组.若整数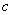 同时满足: 同时满足: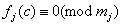
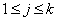 ,则剩余类 ,则剩余类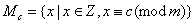 (其中 (其中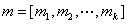 )称为同余方程组的一个解,写作 )称为同余方程组的一个解,写作
定理4:(中国剩余定理)设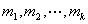 是两两互素的正整数,那么对于任意整数 是两两互素的正整数,那么对于任意整数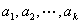 ,一次同余方程组 ,一次同余方程组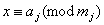 , ,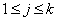 必有解,且解可以写为: 必有解,且解可以写为:
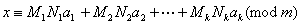
这里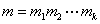 , ,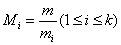 ,以及 ,以及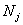 满足 满足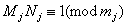 , ,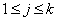 (即 (即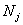 为 为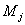 对模 对模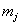 的逆)。 的逆)。
中国定理的作用在于它能断言所说的同余式组当模两两互素时一定有解,而对于解的形式并不重要。
定理5:(拉格郎日定理)设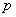 是质数, 是质数, 是非负整数,多项式 是非负整数,多项式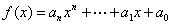 是一个模 是一个模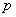 为 为 次的整系数多项式(即 次的整系数多项式(即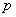 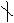  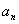 ),则同余方程 ),则同余方程 至多有 至多有 个解(在模 个解(在模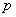 有意义的情况下)。 有意义的情况下)。
定理6:若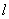 为 为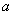 对模 对模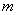 的阶, 的阶, 为某一正整数,满足 为某一正整数,满足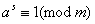 ,则 ,则 必为 必为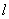 的倍数。 的倍数。
以上介绍的只是一些系统的知识、方法,经常在解决数论问题中起着突破难点的作用。另外还有一些小的技巧则是在解决、思考问题中起着排除情况、辅助分析等作用,有时也会起到意想不到的作用,如: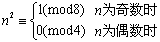 , ,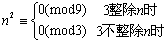 。这里我们只介绍几个较为直接的应用这些定理的例子。 。这里我们只介绍几个较为直接的应用这些定理的例子。
典例分析
例1.设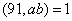 ,求证: ,求证: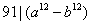 。 。
证明:因为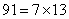 ,故由 ,故由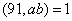 知 知 ,从而 ,从而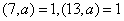 ,但是 ,但是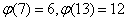 ,故由欧拉定理得: ,故由欧拉定理得: , , ,从而 ,从而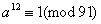 ;同理, ;同理, 。 。
于是, ,即 ,即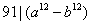 。 。
注明:现考虑整数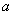 的幂 的幂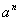 所成的数列: 所成的数列: 若有正整数 若有正整数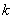 使 使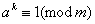 ,则有 ,则有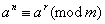 ,其中 ,其中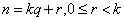 ; ;
因而关于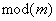 ,数列 ,数列 的项依次同余于 的项依次同余于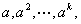 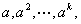 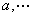 这个数列相继的 这个数列相继的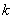 项成一段,各段是完全相同的,因而是周期数列。如下例: 项成一段,各段是完全相同的,因而是周期数列。如下例:
例2.试求不大于100,且使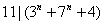 成立的自然数 成立的自然数 的和。 的和。
解:通过逐次计算,可求出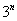 关于 关于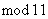 的最小非负剩余(即为被11除所得的余数)为: 的最小非负剩余(即为被11除所得的余数)为:
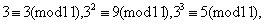 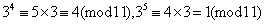
因而通项为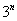 的数列的项的最小非负剩余构成周期为5的周期数列: 的数列的项的最小非负剩余构成周期为5的周期数列:
3,9,5,4,1,3,9,5,4,1,………
类似地,经过计算可得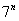 的数列的项的最小非负剩余构成周期为10的周期数列: 的数列的项的最小非负剩余构成周期为10的周期数列:
7,5,2,3,10,4,6,9,8,1,………
于是由上两式可知通项为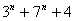 的数列的项的最小非负剩余,构成周期为10(即上两式周期的最小公倍数)的周期数列: 的数列的项的最小非负剩余,构成周期为10(即上两式周期的最小公倍数)的周期数列:
3,7,0,0,4,0,8,7,5,6,………
这就表明,当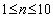 时,当且仅当 时,当且仅当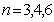 时, 时,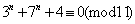 ,即 ,即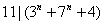 ; ;
又由于数列的周期性,故当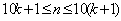 时,满足要求的 时,满足要求的 只有三个,即 只有三个,即
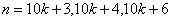
从而当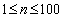 时,满足要求的 时,满足要求的 的和为: 的和为:
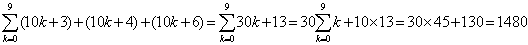 . .
下面我们着重对Fetmat小定理及其应用来举例:
例3.求证:对于任意整数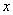 , ,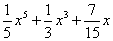 是一个整数。 是一个整数。
证明:令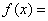 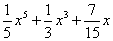 ,则只需证 ,则只需证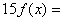 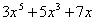 是15的倍数即可。 是15的倍数即可。
由3,5是素数及Fetmat小定理得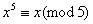 , ,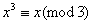 ,则 ,则
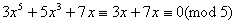 ; ;
而(3,5)=1,故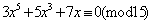 ,即 ,即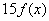 是15的倍数。所以 是15的倍数。所以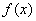 是整数。 是整数。
例4.求证: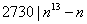 ( ( 为任意整数)。 为任意整数)。
证明:令 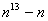 ,则 ,则 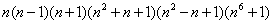 ; ;
所以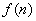 含有因式 含有因式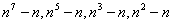
由Fetmat小定理,知13|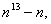 7| 7|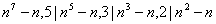
又13,7,5,3,2两两互素,所以2730=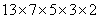 能整除 能整除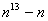 。 。
例5.设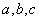 是直角三角形的三边长。如果 是直角三角形的三边长。如果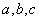 是整数,求证: 是整数,求证: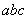 可以被30整除。 可以被30整除。
证明:不妨设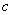 是直角三角形的斜边长,则 是直角三角形的斜边长,则 。 。
若2 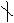  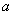 ,2 ,2 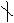  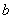 ,2 ,2 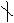  c,则 c,则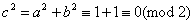 ,又因为 ,又因为 矛盾! 矛盾!
所以2|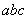 . .
若3 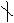  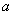 ,3 ,3 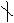  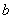 ,3 ,3 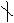  c,因为 c,因为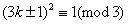 ,则 ,则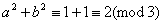 ,又 ,又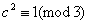 ,矛盾!从而3| ,矛盾!从而3|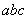 . .
若 5 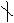  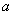 ,5 ,5 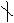  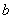 ,5 ,5 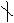  c,因为 c,因为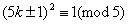 , ,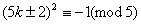 , ,
所以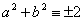 或0(mod5)与 或0(mod5)与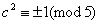 矛盾! 矛盾!
从而5|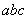 . .
又(2,3,5)=1,所以30|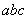 . .
下面讲述中国剩余定理的应用
例6.证明:对于任意给定的正整数 ,均有连续 ,均有连续 个正整数,其中每一个都有大于1的平方因子。 个正整数,其中每一个都有大于1的平方因子。
证明:由于素数有无穷多个,故我们可以取 个互不相同的素数 个互不相同的素数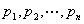 ,而考虑同余组 ,而考虑同余组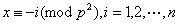 ① ①
因为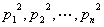 显然是两两互素的,故由中国剩余定理知,上述同余组有正整数解。于是,连续 显然是两两互素的,故由中国剩余定理知,上述同余组有正整数解。于是,连续 个数 个数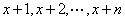 分别被平方数 分别被平方数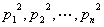 整除。 整除。
注:(1)本题的解法体现了中国剩余定理的一个基本功效,它常常能将“找连续 个正整数具有某种性质”的问题转化为“找 个正整数具有某种性质”的问题转化为“找 个两两互素的数具有某种性质”,而后者往往是比较容易解决的。 个两两互素的数具有某种性质”,而后者往往是比较容易解决的。
(2)本题若不直接使用素数,也中以采用下面的变异方法:由费尔马数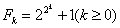 两两互素,故将①中的 两两互素,故将①中的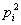 转化为 转化为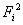  后,相应的同余式也有解,同样可以导出证明。 后,相应的同余式也有解,同样可以导出证明。
例7.证明:对于任意给定的正整数 ,均有连续 ,均有连续 个正整数,其中每一个都不是幂数。 个正整数,其中每一个都不是幂数。
分析:我们来证明,存在连续 个正整数,其中每一个数都至少有一个素因子,在这个数的标准分解中仅出现一次,从而这个数不是幂数。 个正整数,其中每一个数都至少有一个素因子,在这个数的标准分解中仅出现一次,从而这个数不是幂数。
证明:取 个互不相同的素数 个互不相同的素数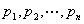 ,考虑同余组 ,考虑同余组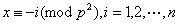
因为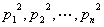 显然是两两互素的,故由中国剩余定理知,上述同余组有正整数解。 显然是两两互素的,故由中国剩余定理知,上述同余组有正整数解。
对于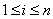 因为 因为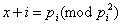 ,故 ,故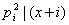 ,但由①式可知 ,但由①式可知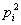   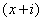 ,即 ,即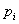 在 在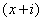 的标准分解中恰好出现一次,故 的标准分解中恰好出现一次,故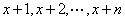 都不是幂数。 都不是幂数。
例8. 设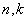 是给定的偶数, 是给定的偶数,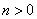 且 且 是偶数。 是偶数。
证明:存在整数 使得 使得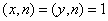 ,且 ,且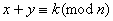 。 。
证明:我们先证明,当 为素数幂 为素数幂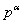 时结论成立。实际上,能够证明,存在 时结论成立。实际上,能够证明,存在 使 使
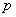 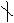   且 且 : :
若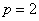 ,则条件表明 ,则条件表明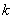 为偶数,此时可取 为偶数,此时可取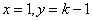 ; ;
若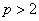 ,则 ,则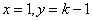 与 与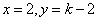 中有一对满足要求。 中有一对满足要求。
一般情形下,设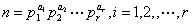 是 是 的一个标准分解,上面已经证明,对每个 的一个标准分解,上面已经证明,对每个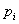 存在整数 存在整数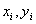 使得 使得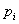    且 且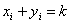 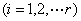 ,而由中国剩余定理, ,而由中国剩余定理,
同余式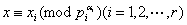 ①有解 ①有解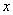 , ,
同余式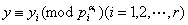 ②有解 ②有解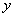 。 。
现不难验证解 符合问题中的要求:因 符合问题中的要求:因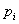 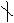   ,故 ,故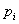 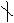   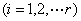 , ,
于是 ,又由①②知 ,又由①②知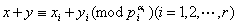 , ,
故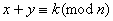 。 。
注:此题的论证表现了中国剩余定理最为基本的作用:将一个关于任意正整数 的问题,化为 的问题,化为 为素数幂的问题,而后者往往是比较好处理的。 为素数幂的问题,而后者往往是比较好处理的。
(责任编辑:admin) |
 ;可用容斥定理来证(证明略)。
;可用容斥定理来证(证明略)。