|
高中数学竞赛讲义（十四） ──极限与导数 一、基础知识 1．极限定义：（1）若数列{un}满足，对任意给定的正数ε，总存在正数m，当n>m且n∈N时，恒有|un-A|<ε成立（A为常数），则称A为数列un当n趋向于无穷大时的极限，记为  ，另外 =A表示x大于x0且趋向于x0时f(x)极限为A，称右极限。类似地 表示x小于x0且趋向于x0时f(x)的左极限。2．极限的四则运算：如果  f(x)=a, g(x)=b，那么[f(x)±g(x)]=a±b, [f(x)?g(x)]=ab,  3.连续：如果函数f(x)在x=x0处有定义，且 f(x)存在，并且f(x)=f(x0)，则称f(x)在x=x0处连续。4．最大值最小值定理：如果f(x)是闭区间[a,b]上的连续函数，那么f(x)在[a,b]上有最大值和最小值。 5．导数：若函数f(x)在x0附近有定义，当自变量x在x0处取得一个增量Δx时（Δx充分小），因变量y也随之取得增量Δy(Δy=f(x0+Δx)-f(x0)).若  存在，则称f(x)在x0处可导，此极限值称为f(x)在点x0处的导数（或变化率），记作 (x0)或 或 ，即 。由定义知f(x)在点x0连续是f(x)在x0可导的必要条件。若f(x)在区间I上有定义，且在每一点可导，则称它在此敬意上可导。导数的几何意义是：f(x)在点x0处导数(x0)等于曲线y=f(x)在点P(x0,f(x0))处切线的斜率。6．几个常用函数的导数：（1）  =0（c为常数）；（2） （a为任意常数）；（3） (4) ;(5) ;(6) ;（7）  ；（8） 7．导数的运算法则：若u(x),v(x)在x处可导，且u(x)≠0,则 （1）  ；（2） ；（3） （c为常数）；（4） ；（5） 。8．复合函数求导法：设函数y=f(u),u=  (x)，已知(x)在x处可导，f(u)在对应的点u(u=(x))处可导，则复合函数y=f[(x)]在点x处可导，且（f[(x)] = .9.导数与函数的性质：（1）若f(x)在区间I上可导，则f(x)在I上连续；（2）若对一切x∈(a,b)有  ，则f(x)在(a,b)单调递增；（3）若对一切x∈(a,b)有 ，则f(x)在(a,b)单调递减。10．极值的必要条件：若函数f(x)在x0处可导，且在x0处取得极值，则  11.极值的第一充分条件：设f(x)在x0处连续，在x0邻域(x0-δ,x0+δ)内可导，（1）若当x∈(x-δ,x0)时  ，当x∈(x0,x0+δ)时 ，则f(x)在x0处取得极小值；（2）若当x∈(x0-δ，x0)时，当x∈(x0,x0+δ)时，则f(x)在x0处取得极大值。12．极值的第二充分条件：设f(x)在x0的某领域(x0-δ,x0+δ)内一阶可导，在x=x0处二阶可导，且  。（1）若 ，则f(x)在x0处取得极小值；（2）若 ，则f(x)在x0处取得极大值。13．罗尔中值定理：若函数f(x)在[a,b]上连续，在(a,b)上可导，且f(a)=f(b)，则存在ξ∈(a,b)，使  [证明] 若当x∈(a,b)，f(x)≡f(a)，则对任意x∈(a,b)，  .若当x∈(a,b)时，f(x)≠f(a)，因为f(x)在[a,b]上连续，所以f(x)在[a,b]上有最大值和最小值，必有一个不等于f(a)，不妨设最大值m>f(a)且f(c)=m，则c∈(a,b)，且f(c)为最大值，故 ，综上得证。14．Lagrange中值定理：若f(x)在[a,b]上连续，在(a,b)上可导，则存在ξ∈(a,b)，使  [证明] 令F(x)=f(x)-  ,则F(x)在[a,b]上连续，在(a,b)上可导，且F(a)=F(b)，所以由13知存在ξ∈(a,b)使 =0，即15．曲线凸性的充分条件：设函数f(x)在开区间I内具有二阶导数，（1）如果对任意x∈I,  ,则曲线y=f(x)在I内是下凸的；（2）如果对任意x∈I, ,则y=f(x)在I内是上凸的。通常称上凸函数为凸函数，下凸函数为凹函数。16．琴生不等式：设α1,α2,…,αn∈R+，α1+α2+…+αn=1。（1）若f(x)是[a,b]上的凸函数，则x1,x2,…,xn∈[a,b]有f(a1x1+a2x2+…+anxn)≤a1f(x1)+a2f(x2)+…+anf(xn). 二、方法与例题 1．极限的求法。 例1 求下列极限：（1）  ；（2） ；（3） ；（4） [解]（1） =  ；（2）当a>1时，  当0<a<1时，  当a=1时，  （3）因为  而 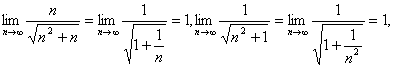 所以  （4）  例2 求下列极限：（1）  (1+x)(1+x2)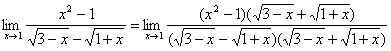(1+ )…(1+ )(|x|<1)；（2）  ；（3） 。[解] （1） (1+x)(1+x2)(1+)…(1+)=  （2）  =  （3）  =   2．连续性的讨论。 例3 设f(x)在(-∞,+∞)内有定义，且恒满足f(x+1)=2f(x)，又当x∈[0,1)时，f(x)=x(1-x)2，试讨论f(x)在x=2处的连续性。 [解] 当x∈[0,1)时，有f(x)=x(1-x)2，在f(x+1)=2f(x)中令x+1=t，则x=t-1，当x∈[1,2)时，利用f(x+1)=2f(x)有f(t)=2f(t-1)，因为t-1∈[0,1),再由f(x)=x(1-x)2得f(t-1)=(t-1)(2-t)2,从而t∈[1,2)时,有f(t)=2(t-1)?(2-t)2；同理，当x∈[1,2)时，令x+1=t，则当t∈[2,3)时，有f(t)=2f(t-1)=4(t-2)(3-t)2.从而f(x)=  所以  ，所以 f(x)= f(x)=f(2)=0，所以f(x)在x=2处连续。3．利用导数的几何意义求曲线的切线方程。 [解] 因为点(2,0)不在曲线上，设切点坐标为(x0,y0)，则  ，切线的斜率为 ，所以切线方程为y-y0= ，即 。又因为此切线过点（2,0），所以 ，所以x0=1，所以所求的切线方程为y=-(x-2)，即x+y-2=0.4．导数的计算。 例5 求下列函数的导数：（1）y=sin(3x+1)；（2）  ；（3）y=ecos2x；（4） ；（5）y=(1-2x)x(x>0且 )。[解] （1）  3cos(3x+1).(2)    （3）  （4）   （5）   5．用导数讨论函数的单调性。 例6 设a>0，求函数f(x)=  -ln(x+a)(x∈(0,+∞))的单调区间。[解]  ，因为x>0,a>0，所以 x2+(2a-4)x+a2>0； x2+(2a-4)x+a+<0.（1）当a>1时，对所有x>0，有x2+(2a-4)x+a2>0，即 (x)>0,f(x)在(0,+∞)上单调递增；（2）当a=1时，对x≠1,有x2+(2a-4)x+a2>0，即，所以f(x)在（0，1）内单调递增，在（1，+∞）内递增，又f(x)在x=1处连续，因此f(x)在(0,+∞)内递增；（3）当0<a<1时，令，即x2+(2a-4)x+a2>0，解得x<2-a- 或x>2-a+，因此，f(x)在(0,2-a-)内单调递增，在(2-a+,+∞)内也单调递增，而当2-a-<x<2-a+时，x2+(2a-4)x+a2<0，即，所以f(x)在(2-a-,2-a+)内单调递减。6．利用导数证明不等式。 例7 设  ，求证：sinx+tanx>2x.[证明] 设f(x)=sinx+tanx-2x，则  =cosx+sec2x-2，当时， （因为0<cosx<1），所以=cosx+sec2x-2=cosx+ .又f(x)在 上连续，所以f(x)在上单调递增，所以当x∈时，f(x)>f(0)=0，即sinx+tanx>2x.7.利用导数讨论极值。 例8 设f(x)=alnx+bx2+x在x1=1和x2=2处都取得极值，试求a与b的值，并指出这时f(x)在x1与x2处是取得极大值还是极小值。 [解] 因为f(x)在(0,+∞)上连续，可导，又f(x)在x1=1，x2=2处取得极值，所以  ，又 +2bx+1，所以 解得 所以  .所以当x∈(0,1)时， ，所以f(x)在(0,1]上递减；当x∈(1,2)时， ，所以f(x)在[1，2]上递增；当x∈(2,+∞)时， ，所以f(x)在[2，+∞）上递减。综上可知f(x)在x1=1处取得极小值，在x2=2处取得极大值。 例9 设x∈[0,π],y∈[0,1]，试求函数f(x,y)=(2y-1)sinx+(1-y)sin(1-y)x的最小值。 [解] 首先，当x∈[0,π],y∈[0,1]时， f(x,y)=(2y-1)sinx+(1-y)sin(1-y)x=(1-y)2x  =(1-y)2x ，令g(x)= , 当  时，因为cosx>0,tanx>x，所以 ；当  时，因为cosx<0,tanx<0,x-tanx>0，所以；又因为g(x)在(0,π)上连续，所以g(x)在(0,π)上单调递减。 又因为0<(1-y)x<x<π，所以g[(1-y)x]>g(x)，即  ，又因为  ，所以当x∈(0,π),y∈(0,1)时，f(x,y)>0.其次，当x=0时，f(x,y)=0；当x=π时，f(x,y)=(1-y)sin(1-y)π≥0. 当y=1时，f(x,y)=-sinx+sinx=0；当y=1时，f(x,y)=sinx≥0. 综上，当且仅当x=0或y=0或x=π且y=1时，f(x,y)取最小值0。 三、基础训练题 1．  =_________.2．已知  ，则a-b=_________.3．  _________.4．  _________.5．计算  _________.6．若f(x)是定义在(-∞,+∞)上的偶函数，且  存在，则 _________.7．函数f(x)在(-∞,+∞)上可导，且  ，则 _________.8．若曲线f(x)=x4-x在点P处的切线平行于直线3x-y=0，则点P坐标为_________. 9．函数f(x)=x-2sinx的单调递增区间是_________. 10．函数  的导数为_________.11．若曲线  在点 处的切线的斜率为 ，求实数a.12.求sin290的近似值。 13．设0<b<a<  ,求证： 四、高考水平练习题 1．计算  =_________.2．计算  _________.3．函数f(x)=2x3-6x2+7的单调递增区间是_________.。 4．函数  的导数是_________.5．函数f(x)在x0邻域内可导，a,b为实常数，若  ，则 _________.6．函数f(x)=  ex(sinx+cosx),x 的值域为_________.7．过抛物线x2=2py上一点(x0,y0)的切线方程为_________. 8．当x>0时，比较大小：ln(x+1) _________x. 9.函数f(x)=x5-5x4+5x3+1,x∈[-1,2]的最大值为_________，最小值为_________. 10．曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴、y轴所围成的三角形面积为S(t)，则S(t)的最大值为_________. 11．若x>0，求证：(x2-1)lnx≥(x-1)2. 12．函数y=f(x)在区间(0,+∞)内可导。导函数 是减函数，且>0，x0∈(0,+∞).y=kx+m是曲线y=f(x)在点(x0,f(x0))处的切线方程，另设g(x)=kx+m，（1）用x0,f(x0), 表示m；（2）证明：当x∈(0,+∞)时，g(x)≥f(x)；（3）若关于x的不等式x2+1≥ax+b≥ 在(0,+∞)上恒成立，其中a,b为实数，求b的取值范围及a,b所满足的关系。13.设各项为正的无穷数列{xn}满足lnxn+  ,证明：xn≤1(n∈N+).五、联赛一试水平训练题 1．设Mn={（十进制）n位纯小数0?  只取0或1（i=1,2,…,n-1），an=1}，Tn是Mn中元素的个数，Sn是Mn中所有元素的和，则 _________.2．若(1-2x)9展开式的第3项为288，则  _________.3．设f(x),g(x)分别是定义在R上的奇函数和偶函数，当x<0时，  ，且g(-3)=0，则不等式f(x)g(x)<0的解集为_________.4．曲线  与 的交点处的切线夹角是_________.5．已知a∈R+，函数f(x)=x2eax的单调递增区间为_________. 6．已知  在(a,3-a2)上有最大值，则a的取值范围是_________.7．当x∈(1,2]时，f(x)=  恒成立，则y=lg(a2-a+3)的最小值为_________.8．已知f(x)=ln(ex+a)(a>0)，若对任意x∈[ln(3a),ln(4a)]，不等式|m-f-1(x)|+ln[ ]<0恒成立，则实数m取值范围是_________.9.已知函数f(x)=ln(1+x)-x,g(x)=xlnx,（1）求函数f(x)的最大值；（2）设0<a<b，证明：0<g(a)+g(b)-  <(b-a)ln2.10.(1)设函数f(x)=xlog2x+(1-x)log2(1-x) (0<x<1)，求f(x)的最小值；（2）设正数p1,p2,…,  满足p1+p2+p3+…+=1，求证：p1log2p1+p2 log2p2+…+log2≥-n.11.若函数gA(x)的定义域A=[a,b)，且gA(x)=  ,其中a,b为任意的正实数，且a<b，（1）求gA(x)的最小值；（2）讨论gA(x)的单调性； （3）若x1∈Ik=[k2,(k+1)2],x2∈Ik+1=[(k+1)2,(k+2)2]，证明：  六、联赛二试水平训练题 1．证明下列不等式：（1）  ；（2）  。2．当0<a≤b≤c≤d时，求f(a,b,c,d)=  的最小值。3．已知x,y∈(0,1)求证：xy+yx>1. 本系列讲座由在人教中数论坛网友“0.1”整理提供，感谢他（她）的分享。 (责任编辑：admin) |