|
高中数学竞赛讲义(十) ──直线与圆的方程 一、基础知识 1.解析几何的研究对象是曲线与方程。解析法的实质是用代数的方法研究几何.首先是通过映射建立曲线与方程的关系,即如果一条曲线上的点构成的集合与一个方程的解集之间存在一一映射,则方程叫做这条曲线的方程,这条曲线叫做方程的曲线。如x2+y2=1是以原点为圆心的单位圆的方程。 2.求曲线方程的一般步骤:(1)建立适当的直角坐标系;(2)写出满足条件的点的集合;(3)用坐标表示条件,列出方程;(4)化简方程并确定未知数的取值范围;(5)证明适合方程的解的对应点都在曲线上,且曲线上对应点都满足方程(实际应用常省略这一步)。 3.直线的倾斜角和斜率:直线向上的方向与x轴正方向所成的小于1800的正角,叫做它的倾斜角。规定平行于x轴的直线的倾斜角为00,倾斜角的正切值(如果存在的话)叫做该直线的斜率。根据直线上一点及斜率可求直线方程。 4.直线方程的几种形式:(1)一般式:Ax+By+C=0;(2)点斜式:y-y0=k(x-x0);(3)斜截式:y=kx+b;(4)截距式: 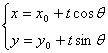 (其中θ为该直线倾斜角),t的几何意义是定点P0(x0, y0)到动点P(x, y)的有向线段的数量(线段的长度前添加正负号,若P0P方向向上则取正,否则取负)。 (其中θ为该直线倾斜角),t的几何意义是定点P0(x0, y0)到动点P(x, y)的有向线段的数量(线段的长度前添加正负号,若P0P方向向上则取正,否则取负)。5.到角与夹角:若直线l1, l2的斜率分别为k1, k2,将l1绕它们的交点逆时针旋转到与l2重合所转过的最小正角叫l1到l2的角;l1与l2所成的角中不超过900的正角叫两者的夹角。若记到角为θ,夹角为α,则tanθ= 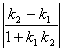 . .6.平行与垂直:若直线l1与l2的斜率分别为k1, k2。且两者不重合,则l1//l2的充要条件是k1=k2;l1 7.两点P1(x1, y1)与P2(x2, y2)间的距离公式:|P1P2|= 8.点P(x0, y0)到直线l: Ax+By+C=0的距离公式: 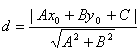 。 。9.直线系的方程:若已知两直线的方程是l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0,则过l1, l2交点的直线方程为A1x+B1y+C1+λ(A2x+B2y+C2=0;由l1与l2组成的二次曲线方程为(A1x+B1y+C1)(A2x+B2y+C2)=0;与l2平行的直线方程为A1x+B1y+C=0( 10.二元一次不等式表示的平面区域,若直线l方程为Ax+By+C=0. 若B>0,则Ax+By+C>0表示的区域为l上方的部分,Ax+By+C<0表示的区域为l下方的部分。 11.解决简单的线性规划问题的一般步骤:(1)确定各变量,并以x和y表示;(2)写出线性约束条件和线性目标函数;(3)画出满足约束条件的可行域;(4)求出最优解。 12.圆的标准方程:圆心是点(a, b),半径为r的圆的标准方程为(x-a)2+(y-b)2=r2,其参数方程为 13.圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)。其圆心为 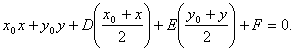 ① ①14.根轴:到两圆的切线长相等的点的轨迹为一条直线(或它的一部分),这条直线叫两圆的根轴。给定如下三个不同的圆:x2+y2+Dix+Eiy+Fi=0, i=1, 2, 3. 则它们两两的根轴方程分别为(D1-D2)x+(E1-E2)y+(F1-F2)=0; (D2-D3)x+(E2-E3)y+(F2-F3)=0; (D3-D1)x+(E3-E1)y+(F3-F1)=0。不难证明这三条直线交于一点或者互相平行,这就是著名的蒙日定理。 二、方法与例题 1.坐标系的选取:建立坐标系应讲究简单、对称,以便使方程容易化简。 例1 在ΔABC中,AB=AC,∠A=900,过A引中线BD的垂线与BC交于点E,求证:∠ADB=∠CDE。 [证明] 见图10-1,以A为原点,AC所在直线为x轴,建立直角坐标系。设点B,C坐标分别为(0,2a),(2a,0),则点D坐标为(a, 0)。直线BD方程为 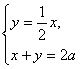 解得点E坐标为 解得点E坐标为所以直线DE斜率为 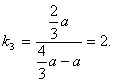 因为k1+k3=0. 因为k1+k3=0.所以∠BDC+∠EDC=1800,即∠BDA=∠EDC。 例2 半径等于某个正三角形高的圆在这个三角形的一条边上滚动。证明:三角形另两条边截圆所得的弧所对的圆心角为600。 [证明] 以A为原点,平行于正三角形ABC的边BC的直线为x轴,建立直角坐标系见图10-2,设⊙D的半径等于BC边上的高,并且在B能上能下滚动到某位置时与AB,AC的交点分别为E,F,设半径为r,则直线AB,AC的方程分别为 所以x1, x2是方程4x2-2mx+m2-r2=0的两根。 由韦达定理 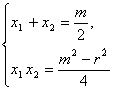 ,所以 ,所以|EF|2=(x1-x2)2+(y1-y2)2=(x1-x2)2+3(x1-x2)2 =4(x1+x2)2-4x1x2=m2-(m2-r2)=r2. 所以|EF|=r。所以∠EDF=600。 2.到角公式的使用。 例3 设双曲线xy=1的两支为C1,C2,正ΔPQR三顶点在此双曲线上,求证:P,Q,R不可能在双曲线的同一支上。 [证明] 假设P,Q,R在同一支上,不妨设在右侧一支C1上,并设P,Q,R三点的坐标分别为 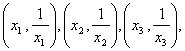 且0<x1<x2<x3. 记∠RQP=θ,它是直线QR到PQ的角,由假设知直线QR,PQ的斜率分别为 且0<x1<x2<x3. 记∠RQP=θ,它是直线QR到PQ的角,由假设知直线QR,PQ的斜率分别为 , , 由到角公式 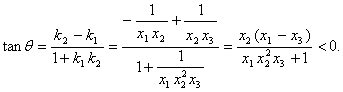 所以θ为钝角,与ΔPQR为等边三角形矛盾。所以命题成立。 3.代数形式的几何意义。 例4 求函数 [解] 因为 4.最值问题。 例5 已知三条直线l1: mx-y+m=0, l2: x+my-m(m+1)=0, l3: (m+1)x-y+m+1=0围成ΔABC,求m为何值时,ΔABC的面积有最大值、最小值。 [解]记l1, l2, l3的方程分别为①,②,③。在①,③中取x=-1, y=0,知等式成立,所以A(-1, 0)为l1与l3的交点;在②,③中取x=0, y=m+1,等式也成立,所以B(0, m+1)为l2与l3的交点。设l1, l2斜率分别为k1, k2, 若m 所以SΔABC= 当m=1时,(SΔABC)max= 5.线性规划。 例6 设x, y满足不等式组 (1)求点(x, y)所在的平面区域; (2)设a>-1,在(1)区域里,求函数f(x,y)=y-ax的最大值、最小值。 [解] (1)由已知得 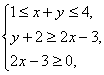 或 或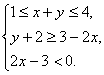 解得点(x, y)所在的平面区域如图10-4所示,其中各直线方程如图所示。AB:y=2x-5;CD:y=-2x+1;AD:x+y=1;BC:x+y=4. (2) f(x, y)是直线l: y-ax=k在y轴上的截距,直线l与阴影相交,因为a>-1,所以它过顶点C时,f(x, y)最大,C点坐标为(-3,7),于是f(x, y)的最大值为3a+7. 如果-1<a≤2,则l通过点A(2,-1)时,f(x, y)最小,此时值为-2a-1;如果a>2,则l通过B(3,1)时,f(x, y)取最小值为-3a+1. 6.参数方程的应用。 例7 如图10-5所示,过原点引直线交圆x2+(y-1)2=1于Q点,在该直线上取P点,使P到直线y=2的距离等于|PQ|,求P点的轨迹方程。 [解] 设直线OP的参数方程为 代入已知圆的方程得t2-t?2sinα=0. 所以t=0或t=2sinα。所以|OQ|=2|sinα|,而|OP|=t. 所以|PQ|=|t-2sinα|,而|PM|=|2-tsinα|. 所以|t-2sinα|=|2-tsinα|. 化简得t=2或t=-2或sinα=-1. 当t=±2时,轨迹方程为x2+y2=4;当sinα=1时,轨迹方程为x=0. 7.与圆有关的问题。 例8 点A,B,C依次在直线l上,且AB=ABC,过C作l的垂线,M是这条垂线上的动点,以A为圆心,AB为半径作圆,MT1与MT2是这个圆的切线,确定ΔAT1T2垂心 的轨迹。 [解] 见图10-6,以A为原点,直线AB为x轴建立坐标系,H为OM与圆的交点,N为T1T2与OM的交点,记BC=1。 以A为圆心的圆方程为x2+y2=16,连结OT1,OT2。因为OT2 又因为OM 点M坐标为(5, b),则点N坐标为 在AB上取点K,使AK= 例9 已知圆x2+y2=1和直线y=2x+m相交于A,B,且OA,OB与x轴正方向所成的角是α和β,见图10-7,求证:sin(α+β)是定值。 [证明] 过D作OD 所以 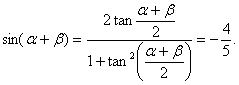 例10 已知⊙O是单位圆,正方形ABCD的一边AB是⊙O的弦,试确定|OD|的最大值、最小值。 [解] 以单位圆的圆心为原点,AB的中垂线为x轴建立直角坐标系,设点A,B的坐标分别为A(cosα,sinα),B(cosα,-sinα),由题设|AD|=|AB|=2sinα,这里不妨设A在x轴上方,则α∈(0,π).由对称性可设点D在点A的右侧(否则将整个图形关于y轴作对称即可),从而点D坐标为(cosα+2sinα,sinα), 所以|OD|= =  因为 当 例11 当m变化且m≠0时,求证:圆(x-2m-1)2+(y-m-1)2=4m2的圆心在一条定直线上,并求这一系列圆的公切线的方程。 [证明] 由 所以 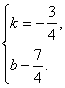 当k不存在时直线为x=1。所以公切线方程y= 当k不存在时直线为x=1。所以公切线方程y=三、基础训练题 1.已知两点A(-3,4)和B(3,2),过点P(2,-1)的直线与线段AB有公共点,则该直线的倾斜角的取值范围是__________. 2.已知θ∈[0,π],则 3.三条直线2x+3y-6=0, x-y=2, 3x+y+2=0围成一个三角形,当点P(x, y)在此三角形边上或内部运动时,2x+y的取值范围是__________. 4.若三条直线4x+y=4, mx+y=0, 2x-3my=4能围成三角形,则m的范围是__________. 5.若λ∈R。直线(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2)的距离为d,比较大小:d__________ 6.一圆经过A(4,2), B(-1,3)两点,且在两个坐标轴上的 四个截距的和为14,则此圆的方程为__________. 7.自点A(-3,3)发出的光线l射到x轴上被x轴反射,其反射光线所在的直线与圆C:x2+y2-4x-4y+7=0相切,则光线l所在的方程为__________. 8.D2=4F且E≠0是圆x2+y2+Dx+Ey+F=0与x轴相切的__________条件. 9.方程|x|-1= 10.已知点M到点A(1,0),B(a,2)及到y轴的距离都相等,若这样的点M恰好有一个,则a可能值的个数为__________. 11.已知函数S=x+y,变量x, y满足条件y2-2x≤0和2x+y≤2,试求S的最大值和最小值。 12.A,B是x轴正半轴上两点,OA=a,OB=b(a<b),M是y轴正半轴上的动点。 (1)求∠AMB的最大值; (2)当∠AMB取最大值时,求OM长; (3)当∠AMB取最大值时,求过A,B,M三点的圆的半径。 四、高考水平训练题 1.已知ΔABC的顶点A(3,4),重心G(1,1),顶点B在第二象限,垂心在原点O,则点B的坐标为__________. 2.把直线 3.M是直线l: 4.以相交两圆C1:x2+y2+4x+y+1=0及C2:x2+y2+2x+2y+1=0的公共弦为直径的圆的方程为__________. 5.已知M={(x,y)|y= 6.圆x2+y2+x-6y+m=0与直线x+2y-3=0交于P,Q两点,O为原点,OP 7.已知对于圆x2+(y-1)2=1上任意一点P(x,y),使x+y+m≥0恒成立,m范围是__________. 8.当a为不等于1的任何实数时,圆x2-2ax+y2+2(a-2)y+2=0均与直线l相切,则直线l的方程为__________. 9.在ΔABC中,三个内角A,B,C所对应的边分别为a,b,c,若lgsinA,lgsinB, lgsinC成等差数列,那么直线xsin2A+ysinA=a与直线xsin2B+ysinC=c的位置关系是__________. 10.设A={(x,y)|0≤x≤2,0≤y≤2},B={(x,y)|x≤10,y≥2,y≤x-4}是坐标平面xOy上的点集,C= 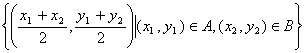 所围成图形的面积是__________. 所围成图形的面积是__________.11.求圆C1:x2+y2+2x+6y+9=0与圆C2:x2+y2-6x+2y+1=0的公切线方程。 12.设集合L={直线l与直线y=2x相交,且以交点的横坐标为斜率}。 (1)点(-2,2)到L中的哪条直线的距离最小? (2)设a∈R+,点P(-2, a)到L中的直线的距离的最小值设为dmin,求dmin的表达式。 13.已知圆C:x2+y2-6x-8y=0和x轴交于原点O和定点A,点B是动点,且∠OBA=900,OB交⊙C于M,AB交⊙C于N。求MN的中点P的轨迹。 五、联赛一试水平训练题 1.在直角坐标系中纵横坐标都是有理数的点称为有理点。若a为无理数,过点(a,0)的所有直线中,每条直线上至少存在两个有理点的直线有_______条。 2.等腰ΔABC的底边BC在直线x+y=0上,顶点A(2,3),如果它的一腰平行于直线x-4y+2=0,则另一腰AC所在的直线方程为__________. 3.若方程2mx2+(8+m2)xy+4my2+(6-m)x+(3m-4)y-3=0表示表示条互相垂直的直线,则m=__________. 4.直线x+7y-5=0分圆x2+y2=1所成的两部分弧长之差的绝对值是__________. 5.直线y=kx-1与曲线y= 6.经过点A(0,5)且与直线x-2y=0, 2x+y=0都相切的圆方程为__________. 7.在直角坐标平面上,同时满足条件:y≤3x, y≥ 8.平面上的整点到直线 9.y=lg(10-mx2)的定义域为R,直线y=xsin(arctanm)+10的倾斜角为__________. 10.已知f(x)=x2-6x+5,满足 11.已知在ΔABC边上作匀速运动的点D,E,F,在t=0时分别从A,B,C出发,各以一定速度向B,C,A前进,当时刻t=1时,分别到达B,C,A。 (1)证明:运动过程中ΔDEF的重心不变; (2)当ΔDEF面积取得最小值时,其值是ΔABC面积的多少倍? 12.已知矩形ABCD,点C(4,4),点A在圆O:x2+y2=9(x>0,y>0)上移动,且AB,AD两边始终分别平行于x轴、y轴。求矩形ABCD面积的最小值,以及取得最小值时点A的坐标。 13.已知直线l: y=x+b和圆C:x2+y2+2y=0相交于不同两点A,B,点P在直线l上,且满足|PA|?|PB|=2,当b变化时,求点P的轨迹方程。 六、联赛二试水平训练题 1.设点P(x,y)为曲线|5x+y|+|5x-y|=20上任意一点,求x2-xy+y2的最大值、最小值。 2.给定矩形Ⅰ(长为b,宽为a),矩形Ⅱ(长为c、宽为d),其中a<d<c<b,求证:矩形Ⅰ能够放入矩形Ⅱ的充要条件是:(ac-bd)2+(ad-bc)2≥(a2-b2)2. 3.在直角坐标平面内给定凸五边形ABCDE,它的顶点都是整点,求证:见图10-8,A1,B1,C1,D1,E1构成的凸五边形内部或边界上至少有一个整点。 4.在坐标平面上,纵横坐标都是整数的点称为整点,试证:存在一个同心圆的集合,使得:(1)每个整点都在此集合的某一圆周上;(2)此集合的每个圆周上,有且只有一个整点。 5.在坐标平面上,是否存在一个含有无穷多条直线l1,l2,…,ln,…的直线族,它满足条件:(1)点(1,1)∈ln,n=1,2,3,…;(2)kn+1≥an-bn,其中kn+1是ln+1的斜率,an和bn分别是ln在x轴和y轴上的截距,n=1,2,3,…;(3)knkn+1≥0, n=1,2,3,….并证明你的结论。 6.在坐标平面内,一圆交x轴正半径于R,S,过原点的直线l1,l2都与此圆相交,l1交圆于A,B,l2交圆于D,C,直线AC,BD分别交x轴正半轴于P,Q,求证: 本系列讲座由在人教中数论坛网友“0.1”整理提供,感谢他(她)的分享。 (责任编辑:admin) |
