|
2010年全国高中数学联赛安徽赛区预赛试卷及详细答案 (考试时间:2010年9月4日9:00—11:30) 注意: 1.本试卷共12小题,满分150分; 2.用钢笔、圆珠笔或签字笔作答; 3.书写不要超过装订线; 4.不能使用计算器. 一、填空题(每小题8分,共64分) 1.函数 2.函数 3.正八面体的任意两个相邻面所成二面角的余弦值等于__________________________. 4.设椭圆 5.设 6.设 7.设 8.从正方体的八个顶点中随机选取三点,构成直角三角形的概率是__________________. 二、解答题(共86分) 9.(20分)设数列 10.(22分)求最小正整数 11.(22分)已知 12.(22分)桌上放有 2010年全国高中数学联赛安徽赛区预赛试卷 参考答案及评分标准 一、填空题(每小题8分,共64分) 1.答案: 提示:因 2. 答案: 提示:因两函数图象关于直线 3. 答案: 提示:正八面体由两个棱长都相等的正四棱锥组成,所以任意两个相邻面所成二面角是正四棱锥侧面与底面所成二面角  4. 答案: 提示:由椭圆方程 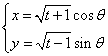 ( (因两曲线相切,∴ 5. 答案: 提示:在复平面上,设 6. 答案: 提示:设三个根为 右边展开与左边比较得 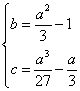 ,这就是所求的充要条件. ,这就是所求的充要条件.7. 答案: 提示:如图,根据向量加法的几何意义,知点 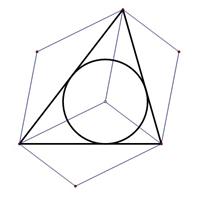 8. 答案: 提示:从正方体的八个顶点中随机选取三点,共有 二、解答题(共86分) 9. 解:特征根法. 又 得 于是 10. 解: 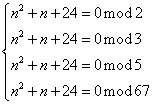 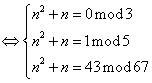 …………(10分) 又 故所求最小正整数 11. 证明:由题设可证 不妨设圆半径为1,则有 由于 ∴ 12. 解:把所有使得甲没有有获胜策略的初始火柴数目 下面我们用数学归纳法证明: (1) (2)当 (3)当 ……………………………………(10分) 设 当 当 当 综上可知, 因为100不在数列 (责任编辑:admin) |
