|
2.2-3总体估计 重难点：会用样本频率分布去估计总体分布，正确地编制频率分布表并能绘制频率直方图、条形图、折线图、茎叶图，体会它们的意义和作用；用样本数据的方差和标准差估计总体的方差与标准差，理解样本数据的方差、标准差的意义和作用，解决一些简单的实际问题． 考纲要求：①了解分布的意义和作用，会列频率分布表，会画频率分布直方图、频率折线图、茎叶图，理解它们各自的特点． ②理解样本数据标准差的意义和作用，会计算数据标准差． ③能从样本数据中提取基本的数字特征（如平均数、标准差），并作出合理的解释． ④会用样本的频率分布估计总体分布，会用样本的基本数字特征估计总体的基本数字特征，理解用样本估计总体的思想． ⑤会用随机抽样的基本方法和样本估计总体的思想，解决一些简单的实际问题． 经典例题：为了了解小学生的体能情况，抽取了某小学同年级部分学生进行跳绳测试，将所得的数据整理后画出频率分布直方图（如下图），已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4.第一小组的频数是5. (1) 求第四小组的频率和参加这次测试的学生人数；(2) 在这次测试中，学生跳绳次数的中位数落在第几小组内？(3) 参加这次测试跳绳次数在100次以上为优秀，试估计该校此年级跳绳成绩优秀率是多少？  当堂练习： 1．10名工人某天生产同一零件，生产的件数是 15 ,17 , 14 , 10 , 15 , 17 ,17 , 16, 14 , 12． 设其平均数为a,中位数为b,众数为c，则有（ ） A．  B． C． D． 2．在用样本估计总体分布的过程中，下列说法正确的是（ ） A．总体容量越大，估计越精确 B．总体容量越小，估计越精确 C．样本容量越大，估计越精确 D．样本容量越小，估计越精确 3．200辆汽车通过某一段公路时的时速的频率分布直方图如右图所示，则时速在[60，70]的汽车大约有（ ） A．30辆 B．40辆 C．60辆 D．80辆 4．对于样本频率直方图与总体密度曲线的关系，下列说法正确的是（ ） A．频率分布直方图与总体密度曲线无关 B．频率分布直方图就是总体密度曲线 C．样本容量很大的频率分布直方图就是总体密度曲线 D．如果样本容量无限增大,分组的组距无限的减小,那么频率分布直方图就会无限接近于总体密度曲线 5．某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，结果用下面的条形图表示． 根据条形图可得这50名学生这一天平均每人的课外阅读时间为（ ） A．0．6小时 B．0．9小时 C．1．0小时 D．1．5小时  6．今有一组实验数据如下：
现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是（ ） A．v=log2t B．v=log  t C．v=  D．v=2t－2 7．已知数据  的平均数为 ，则数据 ， ，…， 的平均数为（ ）A．18 B．22 C．15 D．21 8．若M个数的平均数是X, N个数的平均数是Y,则这M+N个数的平均数是（ ） A．  B． C． D． 9．10个正数的平方和是370，方差是33，那么平均数为（ ） A．1 B．2 C．3 D．4 10．下列说法正确的是（ ） A．甲乙两个班期末考试数学平均成绩相同，这表明这两个班数学学习情况一样 B．期末考试数学成绩的方差甲班比乙班的小，这表明甲班的数学学习情况比乙班好 C．期末考试数学平均成绩甲、乙两班相同，方差甲班比乙班大，则数学学习甲班比乙班好 D．期末考试数学平均成绩甲、乙两班相同，方差甲班比乙班小，则数学学习甲班比乙班好 11．数据a1，a2，a3，…，an的方差为σ2，则数据2a1，2a2，2a3，…，2an的方差为（ ） A．  B．σ2 C．2σ2 D．4σ212．统计量是指不含有任何未知参数的样本的函数。已知  是抽自总体X的一组样本，则①  ；②+1；③ ④ ，其中是统计量的有（ ）个A．1 B．2 C．3 D．4 13．某题的得分情况如下：其中众数是（ ）．
A．37.0％ B．20.2％ C．0分 D．4分 14．从存放号码分别为1，2，…，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码  统计结果如下：
则取到号码为奇数的频率是 ． 15．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如下，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a, b的值分别为 ．  16．期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M:N为 ． 17．数据a1，a2，a3，…，an的方差为σ2，平均数为μ，则数据ka1+b，ka2+b，ka3+b，…，kan+b（kb≠0）的标准差为 ，平均数为 ． 18．(1)完成上面的频率分布表． (2)根据上表，画出频率分布直方图． (3)根据上表，估计数据落在[10.95，11.35]范围内的概率约为多少?
19．在参加世界杯足球赛的32支球队中，随机抽取20名队员，调查其年龄为25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28。填写下面的频率分布表，据此估计全体队员在哪个年龄段的人数最多？占总数的百分之几？并画出频率分布直方图．
20．有一组数据  的算术平均值为10，若去掉其中最大的一个，余下数据的算术平均值为9；若去掉其中最小的一个，余下数据的算术平均值为11．(1) 求出第一个数  关于 的表达式及第个数 关于的表达式．(2)若  都是正整数，试求第个数 的最大值，并举出满足题目要求且取到最大值的一组数据．21．高三年级1000名学生进行数学其中测试。高三年级组随机调阅了100名学生的试卷（满分为150分），成绩记录如下：
求样本平均数和样本方差． 参考答案： 经典例题： 解：(1) 第四小组的频率=1-(0.1+0.3+0.4)=0.2，因为第一小组的频数为5，第一小组的频率为0.1，所以参加这次测试的学生人数为5?0.1=50（人）. (2) 0.3?50=15，0.4?50=20，0.2?50=10，则第一、第二、第三、第四小组的频数分别为5，15，20，10.所以学生跳绳次数的中位数落在第三小组内. (3) 跳绳成绩的优秀率为（0.4+0.2）?100%=60%. 当堂练习： 1.D; 2.D; 3.D; 4.D; 5.B; 6.C; 7.B; 8.C; 9.D; 10.D; 11.D; 12.C; 13.C; 14.  ; 15.27，75; 16. 1; 17. |k|σ kμ+b;18.（1）
（2）   （3）数据落在[10.95，11.35]范围的频率为0.13+0.16+0.26+0.20=0.75， 此数据落在[10.95，11.35]内的概率约为0.75. 19.(1)
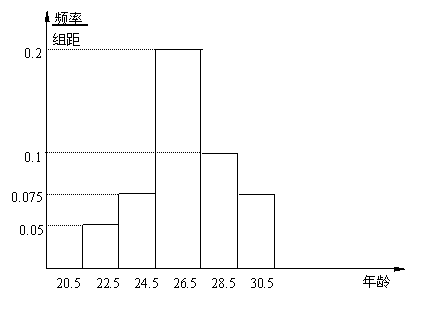(2)   （3）估计全体队员在24.5～26.5处人数最多，占总数的百分之四十. 20. （1） 依条件得：  由 得： ，又由 得： （2）由于  是正整数，故  ， ，故 当 =10时,  ， ， , 此时， , , , , , , , .21. 解：  =6.77  =3.117.(责任编辑：admin) |