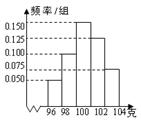
3.(2009山东理)某工厂对一批产品进行了抽样检测.下图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98)，[98，100)，[100，102)，[102，104)，[104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是(      ).
    

A.90          B.75          C.60          D.45
    

考查目的：考查频率分布直方图的阅读与理解能力.
    

答案：A.
    

解析：产品净重小于100克的频率为(0.050+0.100)×2=0.300， 已知样本中产品净重小于100克的个数是36，设样本容量为，则，所以，净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.75，所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.75=90，故选A.
    

 
    二、填空题
    4.对某校高三1200名学生进行体检，得到体重频率分布直方图如图所示，则体重在60kg～70kg之间的学生人数为         ．
    
    考查目的：考查频率分布直方图的阅读与理解能力.
    答案：588.
    解析：(0.042+0.056)×5×1200=588.
    5.(2010北京理)从某小学随机抽取100名同学，将他们的身高(单位：厘米)数据绘制成频率分布直方图(如图). 由图中数据可知      .若要从身高在[120，130)，[130，140)，[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为         .
    
    考查目的：考查频率分布直方图的阅读与理解能力.
    答案：0.030；3.
    解析：(0.005+0.035++0.020+0.010)×10=1，，100×(0.030+0.020+0.010)×10=60，.
    6.(2010福建文)将容量为的样本中的数据分成6组，绘制频率分布直方图.若第一组至第六组数据的频率之比为2︰3︰4︰6︰4︰1，且前三组数据的频数之和等于27，则等于          .
    考查目的：考查频数、频率等有关概念，以及频数、频率的计算.
    答案：60.
    解析：设第一至六组数据的频率分别为，，，，，，则，解得，所以前三组数据的频率分别是，，，故，解得.
    三、解答题
    

7.对某电子元件进行寿命追踪调查，情况如下：
    

⑴列出频率分布表；
    

⑵画出频率分布直方图；
    

⑶估计电子元件寿命在400h以上的频率.
    

考查目的：考查频率分布表和频率分布直方图的意义、绘制和理解，以及用样本估计总体的思想.
    

答案：⑴样本频率分布表如下：
    

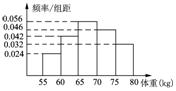
⑵频率分布直方图如图所示：
    

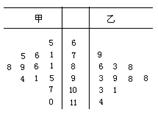
⑶0.35.
    

解析：⑴如答案：⑵作频率分布直方图的步骤：①求极差(数据组中最大值与最小值的差距)；②决定组距与组数；③将数据分组；④列频率分布表；⑤作频率分布直方图(在频率分布表的基础上绘制，横坐标为样本数据尺寸，纵坐标为频率/组距).⑶由频率分布表可知，寿命在400 h以上的电子元件出现的频率为0.20+0.15=0.35，故我们估计电子元件寿命在400 h以上的频率为0.35.
    

8.某中学高二⑵班甲、乙两名同学自高中以来每场数学考试成绩如下：
    

甲：95，81，75，91，86，89，71，65，76，88，94，110，107；
    

乙：83，86，93，99，88，130，98，114，98，79，101.
    

画出两人数学成绩茎叶图，请根据茎叶图对两人的成绩进行比较.
    

考查目的：考查茎叶图的意义、作用和基本特征.
    

答案：甲、乙两人数学成绩的茎叶图如图：
    

从这个茎叶图上可看出，乙同学的得分情况是大致对称的，中位数是99；甲同学的得分情况除一个特殊得分外，也大致对称，中位数是89.因此乙同学发挥比较稳定，总体得分情况比甲同学好.
    解析：在茎叶图中，茎指中间的一列数，叶就是从茎的旁边生长出来的数.中间的数表示得分的十位数，旁边的数分别表示两人得分的个位数.
     (责任编辑：admin)