|
《2.2 用样本估计总体（2）》测试题 一、选择题 1.(2012安徽理)甲、乙两人在一次射击比赛中各射靶5次，两人成绩的条形统计图如图，则( ). 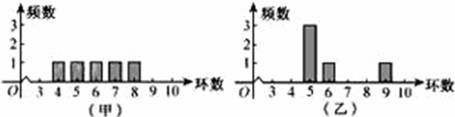 A.甲的成绩的平均数小于乙的成绩的平均数 B.甲的成绩的中位数等于乙的成绩的中位数 C.甲的成绩的方差小于乙的成绩的方差 D.甲的成绩的极差小于乙的成绩的极差 考查目的：考查统计图的识读，以及对数字特征的分析与理解能力. 答案：C. 解析：  ，甲成绩的方差为 ，乙成绩的方差为 .2.(2012江西理)样本(  )的平均数为 ，样本( )的平均数为 ( )，若样本(，)的平均数 ，其中 ，则n，m的大小关系为( ).A.  B. C. D.不能确定考查目的：考查平均数意义的理解和灵活应用. 答案：A. 解析：由题意知，样本( ，)的平均数为 ，又∵，∴ .∵，∴ ，即 ，∴，答案应选A.3.(2012陕西理)从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示(如图)，设甲乙两组数据的平均数分别为  ， ，中位数分别为 ， ，则( ). A.  ， B.， C.  ， D.，考查目的：考查茎叶图的结构特征和作用，以及从茎叶图中提取样本数字特征的能力. 答案：B. 解析：根据平均数的概念易计算出  ，又∵ ， ，∴答案应选B.二、填空题 4.为了解东亚地区14岁男孩的平均体重，现从中国抽取了400个男孩，平均体重为45 kg；从日东抽取了200个男孩，平均体重为40 kg. 从韩国抽取了100个男孩，平均体重41 kg.由此可推断  东亚地区14岁男孩的平均体重为 kg.考查目的：考查平均数的求法，以及用样本估计总体的方法. 答案：43. 解析：  .5.(2010江苏)某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标)，所得数据都在区间[5，40]中，其频率分布直方图如图所示，则其抽样的100根中，有_ ___根在棉花纤维的长度小于20mm.  考查目的：考查频率分布直方图的识读与理解能力. 答案：30. 解析：100×(0.001+0.001+0.004)×5=30. 6.(2011江苏)某老师  从星期一到星期五收到信件数分别是10，6，8，5，6，则该组数据的方差 .考查目的：考查方差的定义及计算公式的应用. 答案:3.2. 解析：平均数为
问：哪种小麦长得比较整齐？ 考查目的：考查平均数、方差等特征数字在分析和解决实际问题中的作用. 答案：甲种麦比较整齐. 解析：平均数对数据有“取齐”的作用，代表一组数据的平均水平.用样本平均数可以估计总体平均数.方差( 标准差)描述一组数据围绕平均数波动的大小，反映了一组数据变化的幅度.即反映了数据距离平均数的离散程度.标准差较大，数据的离散程度较大；标准差较小，数据的离散程度较小.用样本方差(标准差)可以估计总体方差(标准差).样本容量越大，估计就越精确. ∵  ， ，∴ ，故需要比较两种小麦的方差，而 ，显然 ，所以甲种麦比较整齐.8.(2010安徽)某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物): 61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，91，77，86，81，83，82，82，64，79，86，85，75，71，49，45. ⑴完成频率分布表； ⑵作出频率分布直方图； ⑶根据国家标准，污染指数在0～50之间时，空气质量为优：在51～100之间时，为良；在101～150之间时，为轻微污染；在151～200之间时，为轻度污染. 请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价. 考查目的：考查频数，频率的概念及频率分布直方图的意义和作用，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识.
答案：⑴频率分布表如上表：⑵频率分布直方图下图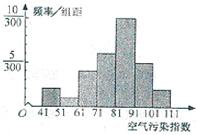：  ⑶答对下述两条中的一条即可： ①该市一个月中空气污染指数有2天处于优的水平，占当月天数的  ，有26天处于良的水平，占当月天数的 ，处于优或良的天数共有28天，占当月天数的 .说明该市空气质量基本良好.②轻微污染有2天，占当月天数的 .污染指数在80以上的接近轻微污染的天数有15天，加上处于轻微污染的天数，共有17天，占当月天数的 ，超过50%，说明该市空气质量有待进一步改善.解析：首先根据题目中的数据完成频率分布表，作出频率分布直方图，根据污染指数，确定空气质量为优、良、轻微污染、轻度污染的天数.在频率分布表中，频数的和等于样本容量，频率的和等于1，每一小组的频率等于这一组的频数除以样本容量.频率分布直方图中，小矩形的高等于每一组的频率/组距，它们与频数成正比，小矩形的面积等于这一组的频率. (责任编辑：admin) |
，
.
