|
2.4线性回归方程 重难点：散点图的画法，回归直线方程的求解方法，回归直线方程在现实生活与生产中的应． 考纲要求：①会作两个有关联变量数据的散点图，会利用散点图认识变量间的相关关系． ②了解最小二乘法的思想，能根据给出的线性回归方程系数公式建立线性回归方程． 经典例题：10．有10名同学高一（x）和高二（y）的数学成绩如下：
⑴画出散点图； ⑵求y对x的回归方程。 当堂练习： 1.下表是某小卖部一周卖出热茶的杯数与当天气温的对比表：若热茶杯数y与气温x近似地满足线性关系，则其关系式最接近的是（ ）
A．  B． C． D． 2．线性回归方程  表示的直线必经过的一个定点是（ ）A．  B．  C．  D．  3．设有一个直线回归方程为  ,则变量x 增加一个单位时 （ ）A． y 平均增加 1.5 个单位 B. y 平均增加 2 个单位 C． y 平均减少 1.5 个单位 D. y 平均减少 2 个单位 4．对于给定的两个变量的统计数据，下列说法正确的是（ ） A．都可以分析出两个变量的关系 B．都可以用一条直线近似地表示两者的关系 C．都可以作出散点图 D. 都可以用确定的表达式表示两者的关系 5．对于两个变量之间的相关系数，下列说法中正确的是（ ） A．|r|越大，相关程度越大 B．|r|  ，|r|越大，相关程度越小，|r|越小，相关程度越大C．|r|  1且|r|越接近于1，相关程度越大；|r|越接近于0，相关程度越小D．以上说法都不对 6．“吸烟有害健康”，那么吸烟与健康之间存在什么关系（ ） A．正相关 B．负相关 C．无相关 D．不确定 7．下列两个变量之间的关系不是函数关系的是（ ） A．角度与它的余弦值 B．正方形的边长与面积 C．正n边形的边数和顶点角度之和 D．人的年龄与身高 8．对于回归分析，下列说法错误的是（ ） A．变量间的关系若是非确定性关系，则因变量不能由自变量唯一确定 B．线性相关系数可正可负 C．如果  ，则说明x与y之间完全线性相关D．样本相关系数  9．为了考察两个变量x和y之间的线性相关性，甲、乙两个同学各自独立的做10次和15V次试验，并且利用线性回归方法，求得回归直线分布为  和 ，已知在两人的试验中发现对变量x的观察数据的平均值恰好相等都为s，对变量y的观察数据的平均值恰好相等都为t,那么下列说法正确的是（ ）A．直线 和有交点（s,t） B．直线和相交，但是交点未必是（s,t）C． 直线 和平行 D． 直线和必定重合10．下列两个变量之间的关系是相关关系的是（ ） A．正方体的棱长和体积 B．单位圆中角的度数和所对弧长 C．单产为常数时，土地面积和总产量 D．日照时间与水稻的亩产量 11．对于简单随机抽样，下列说法中正确的命题为（ ） ①它要求被抽取样本的总体的个数有限，以便对其中各个个体被抽取的概率进行分析；②它是从总体中逐个地进行抽取，以便在抽取实践中进行操作；③它是一种不放回抽样；④它是一种等概率抽样，不仅每次从总体中抽取一个个体时，各个个体被抽取的概率相等，而且在整个抽样过程中，各个个体被抽取的概率也相等，从而保证了这种方法抽样的公平性. A．①②③ B．①②④ C．①③④ D．①②③④ 12．为了解初一学生的身体发育情况，打算在初一年级10个班的某两个班按男女生比例抽取样本，正确的抽样方法是（ ） A．随机抽样 B．分层抽样 C．先用抽签法，再用分层抽样 D．先用分层抽样，再用随机数表法 13．下列调查中属于样本调查的是（ ） ①每隔5年进行一次人口普查 ②某商品的优劣 ③某报社对某个事情进行舆论调查 ④高考考生的体查 A．②③ B．①④ C. ③④ D. ①② 14．现实世界中存在许多情况是两个变量间有密切联系,但这种关系无法用确定的函数关系式表达出来,这种变量之间的关系称 ． 15．江苏某中学高一期中考试后，对成绩进行分析，从13班中选出5名学生的总成绩和外语成绩如下表:
则外语成绩对总成绩的回归直线方程是 ． 16．对于回归方程y=4.75x+257,当x=28时,y的估计值为 ． 17．相应与显著性水平0.05,观测值为10组的相关系数临界值为 ． 18．假设关于某设备的使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：
若由资料知，y对x呈线性相关关系，试求： （1）回归直线方程； （2）估计使用年限为10年时，维修费用约是多少？ 19．假设关于某设备的使用年限  和所支出的维修费用 (万元),有如下的统计数据 由资料知对呈线性相关,并且统计的五组数据得平均值分别为 , ,若用五组数据得到的线性回归方程 去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,求回归直线方程;(2)估计使用年限为10年时,维修费用是多少? 20．某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
(1)画出销售额和利润额的散点图．(2)若销售额和利润额具有相关关系，计算利润额y对销售额x的回归直线方程．(3)对计算结果进行简要的分析说明． 21．已知10只狗的血球体积及红血球的测量值如下
ｘ（血球体积，ｍｍ），ｙ（血红球数，百万） 画出上表的散点图;(2)求出回归直线并且画出图形  （3）回归直线必经过的一点是哪一点？参考答案： 经典例题：10．解： ⑴如图：   ⑵ 由已知表格的数据可得，  ， 所以，   又可查表中相应与显著性水平0.05和n－2的相关系数的临界值  因为  可知,y与x具有相关关系.因为y与x具有相关关系，设y=bx+a， ∴  ∴所求的回归方程为y=1.22x－14.32． 当堂练习： 1.C; 2.D; 3.C; 4.C; 5.B; 6.B; 7.D; 8.D; 9.A; 10.D; 11.D; 12.C; 13.C; 14. 相关关系; 15.  =14.5+0.132; 16. 390; 17. 0.632;18.（1）列表如下：
  ∴回归直线方程为  （2）当  时， （万元）即估计用10年时，维修费用约为12.38万元。 19.(1)因为线性回归方程 经过定点 ,将 , 代入回归方程得 ; 又 ;解得 , 线性回归方程 (2)将  代入线性回归方程得 (万元)∴线性回归方程 ;使用年限为10年时,维修费用是21(万元).．20.（1）如下图： （2）y=0.5x+0.4 （3）略 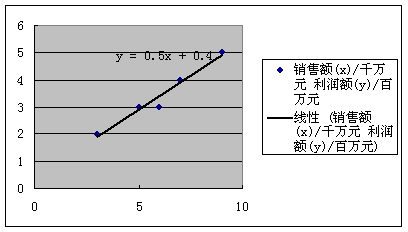 21.解：（１）见下图 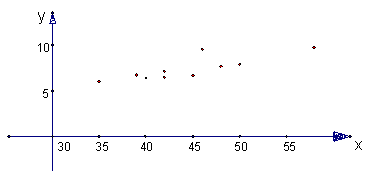 （２）   设回归直线为 ，所以所求回归直线的方程为 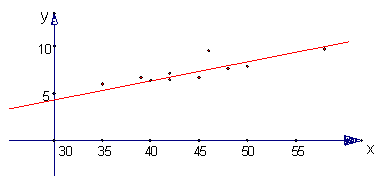 ，图形如下: 回归直线必过点（45.50,7.37）. (责任编辑：admin) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
