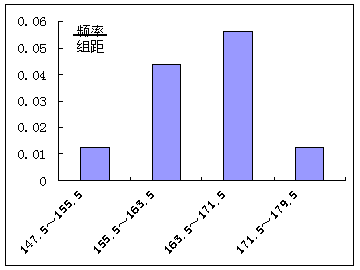
|
必修3综合测试 1．某社区有400个家庭，其中高等收入家庭120户，中等收入家庭180户，低收入家庭100户.为了调查社会购买力的某项指标，要从中抽取一个容量为100的样本记作①；某校高一年级有12名女排球运动员，要从中选出3人调查学习负担情况，记作②；那么，完成上述2项调查应采用的抽样方法是（ ） A．①用随机抽样法，②用系统抽样法 B．①用分层抽样法，②用随机抽样法 C．①用系统抽样法，②用分层抽样法 D．①用分层抽样法，②用系统抽样法 2．要从已编号（1～60）的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是（ ） A．5，10，15，20，25，30 B．3，13，23，33，43，53 C．1，2，3，4，5，6 D．2，4，8，16，32，48 3．数据70，71，72，73的标准差是（ ） A．2 B．  C． D． 4．数据a1，a2，a3，…，an的方差为σ2，则数据2a1，2a2，2a3，…，2an的方差为（ ） A．  B．σ2 C．2σ2 D．4σ25．下面的伪代码输出的结果是（ ） A． 3 B． 5 C． 9 D ．13  6．一个容量为40的样本数据分组后组数与频数如下：［25，25.3），6；［25.3，25.6），4；［25.6，25.9），10；［25.9，26.2），8；［26.2，26.5），8；［26.5，26.8），4；则样本在［25，25.9）上的频率为（ ） A．  B． C． D． 7．设有一个直线回归方程为y=2－1.5x，则变量x增加一个单位时（ ） A．y平均增加1.5个单位 B．y平均增加2个单位 C．y平均减少1.5个单位 D．y平均减少2个单位 8．如图所示，在两个圆盘中，指针落在本圆盘每个数所在区域的机会均等，那么两个指针同时落在奇数所在区域的概率是（ ） A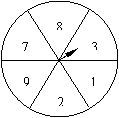．  B． C．  D．   9．某班30名同学，一年按365天计算，至少有两人生日在同一天的概率是（ ） A．  B． C． D． 10．甲乙两人下棋，甲获胜的概率为40%，甲不输的概率为90%，则甲乙下成和棋的概率为（ ） A．60% B．30% C．10% D．50% 11．将数字1、2、3填入标号为1，2，3的三个方格里，每格填上一个数字，则方格的标号与所填的数字有相同的概率是（ ） A．  B． C． D． 12． 3名老师随机从3男3女共6人中各带2名学生进行实验，其中每名老师各带1名男生和1名女生的概率为（ ） A．  B． C． D． 13．掷两颗骰子，出现点数之和等于8的概率等于__________． 14．为了了解参加运动会的2000名运动员的年龄情况，从中抽取100名运动员；就这个问题，下列说法中正确的有 ． ①2000名运动员是总体；②每个运动员是个体；③所抽取的100名运动员是一个样本；④样本容量为100；⑤这个抽样方法可采用按年龄进行分层抽样；⑥每个运动员被抽到的概率相等． 15. 某公司有1000名员工，其中：高层管理人员占5％，中层管理人员占15％，一般员工占80％，为了了解该公司的某种情况，现用分层抽样的方法抽取120名进行调查，则一般员工应抽取 人． 16. 从长度分别为1，2，3，4的四条线段中，任取三条的不同取法共有n种，在这些取法中，以取出的三条线段为边可组成的三角形的个数为m，则  等于 ．17．某同学在高考报志愿时，报了4所符合自己分数和意向的高校，若每一所学校录取的概率为 ，则这位同学被其中一所学校录取的概率为 ．18．我国古代数学发展一直处于世界领先水平，特别是宋、元时期的“算法”，其中可以同欧几里德辗转相除法相媲美的是 ． 19．对某校初二男生抽取体育项目俯卧撑，被抽到的50名学生的成绩如下：
试求全校初二男生俯卧撑的平均成绩． 20．为了解某地初三年级男生的身高情况，从其中的一个学校选取容量为60的样本(60名男生的身高)，分组情况如下：
(1)求出表中的a,m的值． (2)画出频率直方图． 21.某人玩硬币走跳棋的游戏，已知硬币出现正、反面的概率都是 ．棋盘上标有第0站、第1站、第2站、……、第100站．一枚棋子开始在第0站，棋手每掷一次硬币，棋子向前跳动一次，若掷出正面，棋子向前跳一站；若掷出反面，则棋子向前跳两站，直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时，该游戏结束．设棋子跳到第n站的概率为Pn．(I)求P0，Pl，P2；(II)求证:  ； (Ⅲ)求玩该游戏获胜的概率．22．目前高中毕业会考中，成绩在85～100为“A”,70～84为“B”,60～69为“C”,60分以下为“D”.编制程序，输入学生的考试成绩(百分制，若有小数则四舍五入)，输出相应的等级． 23．甲、乙两艘轮船都要停靠同一个泊位，它们可以在一昼夜的任意时刻到达，设甲、乙两艘轮船停靠泊位的时间分别是3小时和5小时，求有一艘轮船停靠泊位时必须等待一段时间的概率． 参考答案： 1.B; 2.B; 3.D; 4.D; 5.C; 6.C; 7.C; 8.A; 9.A; 10.D; 11.D; 12.A; 13. ; 14. ④⑥; 15. 96; 16.  ; 17.  ; 18. 更相减损术; 19.7.2次.20.（1）m=6；a=0.45.（2）
21.解：(I)依题意，得 P0=1 P1=   (II)依题意，棋子跳到第n站(2≤n≤99)有两种可能：第一种，棋子先到第n-2站，又掷出反面，其概率为  ；第二种，棋子先到第n-1站，又掷出正面，其概率为 ∴  ∴  即  …….9分(III)由(II)可知数列{  }(1≤n≤99)是首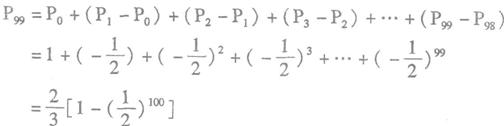项为 公比为 的等比数列， 于是有  因此，玩该游戏获胜的概率为  .22.I=1 WHILE I=1 INPUT “shu ru xue sheng cheng ji a=”;a IF a<60 THEN PRINT “D” ELSE IF a<70 THEN PRINT “C” ELSE IF a<85 THEN  PRINT “B”ELSE PRINT “A” END IF END IF END IF INPUT “INPUT 1，INPUT 2”；I WEND END 23.解：以甲船到达泊位的时刻x，乙船到达泊位的时刻y分别为坐标轴，则 由题意知 0≤x，y≤24 设事件A={有一艘轮船停靠泊位时必须等待一段时间}，事件B={甲船停靠泊位时必须等待一段时间}，事件C={乙船停靠泊位时必须等待一段时间} 则A= B∪C，并且事件B与事件C是互斥事件 ∴P(A)= P(B∪C)= P(B)+ P(C) 而甲船停靠泊位时必须等待一段时间需满足的条件是0<x-y≤5，乙船停靠泊位时必须等待一段时间需满足的条件是0<y-x≤3， 在如图所示的平面直角坐标系下，点（x，y）的 所有可能结果是边长为24的正方形，事件A的可能 结果由图中的阴影部分表示，则S正方形=242=576 S阴影=242- 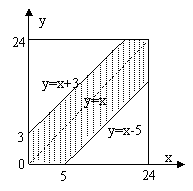×(24-5)2-×(24-3)2 =175  ∴由几何概率公式得P(A)=  ∴有一艘轮船停靠泊位时必须等待一段时间的概率是 . (责任编辑：admin) |
