|
《2.1 点、直线、平面之间的位置关系》测试题 一、选择题 1.(2011四川)  ， ， 是空间三条不同的直线，则下列命题正确的是( ).A. ⊥，⊥?∥ B.⊥，∥?⊥C. ∥∥?，，共面 D.，，共点?，，共面考查目的：考查空间中直线与直线的位置关系及有关性质. 答案：B. 解析：在空间中，垂直于同一直线的两条直线有可能相交或异面，故A错；两平行线中的一条垂直于第三条直线，则另一条也垂直于第三条直线，B正确；相互平行的三条直线不一定共面，如三棱柱的三条侧棱，故C错；共点的三条直线不一定共面，如三棱锥的三条侧棱，故D错. 2.若三个平面两两相交，有三条交线，且三条交线互相平行，则这三个平面把空间分成( ). A.5部分 B.6部分 C.7部分 D.8部分 考查目的：考查空间平面的位置关系和空间想象能力. 答案：C. 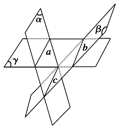 解析：如图所示，三个平面  ， ， 两两相交，交线分别是 ， ， ，且∥∥.观察图形，可得，，把空间分成7部分.3.(2010重庆文)到两条互相垂直的异面直线的距离相等的点( ). A.只有1个 B.恰有3个 C.恰有4个 D.有无穷多个  考查目的：考查异面直线的概念、性质和空间想象能力. 答案：D. 解析：可以将异面直线放在正方体中研究，显然，线段  、EF、FG、GH、HE的中点到两垂直异面直线AB、CD的距离都相等，所以排除A、B、C，选D.也可以在四条侧棱上找到四个点到两垂直异面直线AB、CD的距离相等.二、填空题 4.(2010江西改编)过正方体  的顶点A作直线 ，使与棱AB，AD， 所成的角都相等，这样的直线可以作_______.A.1条 B.2条 C.3条 D.4条 考查目的：考查空间直线所成的角概念与求法. 答案：8.  解析：如图，连结体对角线  ，显然与棱AB、AD，所成的角都相等，所成角的正切值都为 .联想正方体的其他体对角线，如连结 ，则与棱BC、BA、 所成的角都相等，∵∥，BC∥AD，∴体对角线与棱AB、AD、所成的角都相等，同理，体对角线 、 也与棱AB、AD、所成的角都相等，过A点分别作、、的平行线都满足题意，故这样的直线可以作4条.5.正方体 中，P、Q、R分别是AB、AD、 的中点，那么，正方体的过P、Q、R的截面图形是 .考查目的：考查空间几何的公理３，判断空间点线的共面关系. 答案：六边形. 解析：如图，作RG∥PQ交  于G，连接QP并延长与CB交于M，连接MR交于E，连接PE、RE为截面的部分外形．同理连PQ并延长交CD于N，连接NG交 于F，连接QF，FG，∴截面为六边形PQFGRE. 6.(2012安徽文)若四面体  的三组对棱分别相等，即 ， ， ，则____________(写出所有正确结论编号). ①四面体 每组对棱相互垂直②四面体 每个面的面积相等③从四面体 每个顶点出发的三条棱两两夹角之和大于 而小于 ④连接四面体 每组对棱中点的线段互垂直平分⑤从四面体 每个顶点出发的三条棱的长可作为一个三角形的三边长考查目的：考查空间直线与直线的位置关系. 答案：②④⑤. 解析：①连接四面体 每组对棱中点构成菱形；②四面体每个面是全等三角形，面积相等； ③从四面体每个顶点出发的三条棱两两夹角之和等于； ④连接四面体每组对棱中点构成菱形，菱形对角线垂直平分；⑤连结四面体棱 的中点 可得 ，该三角形三边分别等于长度的一半.三、解答题 7.正方体 中，E、F分别是AB和的中点．求证：⑴E，C，  ，F四点共面；⑵CE，  ，DA三线共点. 考查目的：考查空间几何公理，会证明共线、共面问题. 解析：⑴如图，连接EF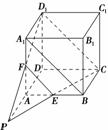，  ， .∵E、F分别是AB、 的中点，∴EF∥ .又∵∥ ，∴EF∥，∴E、C、 、F四点共面.⑵∵EF∥ ，EF＜，∴CE与 必相交.设交点为P，则由P∈CE，CE?平面ABCD，得P∈平面ABCD.同理P∈平面 .又∵平面ABCD∩平面＝DA，∴P∈直线DA，∴CE、、DA三线共点. 8.A是△BCD平面外的一点，E，F分别是BC，AD的中点. ⑴求证：直线EF与BD是异面直线； ⑵若AC⊥BD，AC＝BD，求EF与BD所成的角. 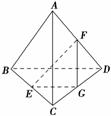 考查目的：考查异面直线的判定，求异面直线所成角的基本方法. 答案：⑴略；⑵  .解析：⑴假设EF与BD不是异面直线，则EF与BD共面，从而DF与BE共面，即AD与BC共面，所以A、B、C、D在同一平面内，这与A是△BCD平面外的一点相矛盾，故直线EF与BD是异面直线. ⑵如图，设G为CD的中点，连接EG、FG，则EG∥BD，所以相交直线EF与EG所成的  ，即等于异面直线EF与BD所成的角.同理 即为异面直线AC和BD所成的角，又∵AC⊥BD，∴为直角，在Rt△EGF中，由EG＝FG＝ AC，求得∠FEG＝，即异面直线EF与BD所成的角为.(责任编辑：admin) |