|
《2.3 直线、平面垂直的判定及其性质（2）》测试题 一、选择题 1.(2010山东)在空间中，下列命题正确的是( )． A.平行直线的平行投影重合 B.平行于同一直线的两个平面平行 C.垂直于同一平面的两个平面平行 D.垂直于同一平面的两条直线平行 考查目的：考查空间直线与平面的位置关系，直线与平面垂直、平行的判定和性质. 答案：D. 解析：选项A，平行直线的平行投影可以依然是两条平行直线；选项B，两个相交平面的交线与某一条直线平行，则这条直线平行于这两个平面；选项C，两个相交平面可以同时垂直于同一个平面；选项D正确. 2.(2012浙江文)设  是直线， ， 是两个不同的平面，则下列结论正确的是( ).A.若 ∥，∥，则∥ B.若∥，⊥，则⊥C.若 ⊥，⊥，则⊥ D.若⊥，∥，则⊥考查目的：考查直线与平面平行、垂直的判定和性质. 答案：B. 解析：利用排除法可得选项B是正确的，选项A：当 ∥，∥时，⊥或∥；选项C：若⊥，⊥，则∥或 ；选项D：若⊥，⊥，则∥或⊥.3.(2010全国2文)已知三棱锥 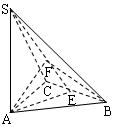 中，底面 为边长等于2的等边三角形， 垂直于底面， ，那么直线 与平面 所成角的正弦值为( ).A.  B. C. D.  考查目的：考查直线与平面、平面与平面的位置关系，会求直线与平面所成的角. 答案：D. 解析：过A作AE垂直于BC交BC于E，连结SE，过A作AF垂直于SE交SE于F，连BF，∵正三角形ABC，∴ E为BC中点，∵BC⊥AE，SA⊥BC，∴BC⊥面SAE，∴BC⊥AF，AF⊥SE，∴AF⊥面SBC，∵∠ABF为直线AB与面SBC所成角，由正三角形边长3，∴  ，AS=3，∴ ， ，∴ .二、填空题 4.(2010辽宁理)如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______. 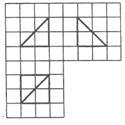 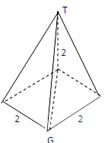 考查目的：考查直线与平面垂直的判定. 答案：  .解析：由三视图可知，此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥，所以最长棱长为  .5.(2010四川)如图，二面角 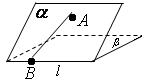 的大小是 ，线段 . ，与所成的角为 ，则与平面 所成的角的正弦值是 . 考查目的：考查直线和平面所成角的概念和求法. 答案： .解析：过点A作平面 的垂线，垂足为C，在内过C作的垂线.垂足为D.连结AD，则 平面 ，AD⊥，故∠ADC为二面角的平面角为.又由已知得，∠ABD＝，连结CB，则∠ABC为与平面所成的角.设AD＝2，则 ，CD＝1， ，∴ . 6.(2012上海理)如图，  与 是四面体 中互相垂直的棱， ，若 ，且 ，其中 ， 为常数，则四面体的体积的最大值是 . 考查目的：考查直线与直线、直线与平面垂直关系，会根据几何体特点进行合理的计算. 答案：  .解析：过点A做AE⊥BC，垂足为E，连接DE，由AD⊥BC可知，BC⊥平面ADE，所以  .又∵，∴当 时，四面体ABCD的体积最大.过E做EF⊥DA，垂足为点F，已知EA=ED，∴△ADE为等腰三角形，∴点E为AD的中点.又∵ ，∴ ，∴ ，∴四面体ABCD体积的最大值 .三、解答题 7.(2011天津改编)如图，在四棱锥  中，底面 为平行四边形， ， ，O为AC中点， ⊥平面，PO=2，M为PD中点，求直线AM与平面ABCD所成角的正切值. 考查目的：考查直线和平面所成角的概念及其求法. 答案：  .解析：取DO中点N，连接MN，AN.∵M为PD的中点，∴MN∥PO，且  .由PO⊥平面ABCD，得MN⊥平面ABCD，∴ 是直线AM与平面ABCD所成的角.在 中， ， ，∴ ，∴ ．在 中， ．即直线AM与平面ABCD所成角的正切值为．8.(2010辽宁文)如图，棱柱  的侧面 是菱形， . ⑴证明：平面   平面 ；⑵设  是 上的点，且 平面 ，求 的值.考查目的：考查空间直线、平面之间的平行、垂直关系的证明，以及二面角的求法. 答案：C. 解析：⑴∵侧面 是菱形，∴ .又∵，且 ，∴ 平面.∵ 平面，∴平面 平面.⑵设  交 于点E，连结DE，则DE是平面与平面的交线. ∵ ∥平面，∴ .又∵E是的中点，∴以D为的中点，∴ . (责任编辑：admin) |