|
1.2点、线、面之间的位置关系 考纲要求：①理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理． ◆公理1：如果一条直线上的两点在一个平面内，这条直线上所有的点在此平面内． ◆公理2：过不在同一条直线上的三点，有且只有一个平面． ◆公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线． ◆公理4：平行于同一条直线的两条直线互相平行． ◆定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补． ②以立体几何的上述定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定． 理解以下判定定理． ◆如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行． ◆如果一个平面内的两条相交直线与另一个平面都平行，那么这两个平面平行． ◆如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直． ◆如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直． 理解以下性质定理，并能够证明． ◆如果一条直线与一个平面平行，经过该直线的任一个平面与此平面相交，那么这条直线就和交线平行． ◆如果两个平行平面同时和第三个平面相交，那么它们的交线相互平行． ◆垂直于同一个平面的两条直线平行． ◆如果两个平面垂直，那么一个平面内垂直于它们交线的直线于另一个平面垂直． ③能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题． 1.2.1 平面的基本性质 重难点：理解平面的概念及表示，掌握平面的基本性质并注意他们的条件、结论、作用、图形语言及符号语言． 经典例题： 如图，设E，F，G，H，P，Q分别是正方体ABCD-A1B1C1D1 所在棱上的中点，求证：E，F，G，H，P，Q共面. 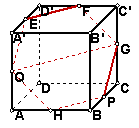 当堂练习： 1．下面给出四个命题： ①一个平面长4m, 宽2m; ②2个平面重叠在一起比一个平面厚; ③一个平面的面积是25m2; ④一条直线的长度比一个平面的长度大, 其中正确命题的个数是（ ） A． 0 B．1 C．2 D．3 2．若点N在直线a上，直线a又在平面  内，则点N，直线a与平面之间的关系可记作（ ）A．N  B．N C．N D．N 3． 空间不共线的四点，可以确定平面的个数为（ ） A．0 B．1 C．1或4 D． 无法确定 4． 空间 四点A，B，C，D共面但不共线，则下面结论成立的是（ ） A． 四点中必有三点共线 B． 四点中必有三点不共线 C．AB，BC，CD，DA四条直线中总有两条平行 D． 直线AB与CD必相交 5． 空间不重合的三个平面可以把空间分成（ ） A． 4或6或7个部分 B． 4或6或7或8个部分 C． 4或7或8个部分 D． 6或7或8个部分 6．下列说法正确的是（ ） ①一条直线上有一个点在平面内, 则这条直线上所有的点在这平面内; ②一条直线上有两点在一个平面内, 则这条直线在这个平面内; ③若线段AB  , 则线段AB延长线上的任何一点一点必在平面 内; ④一条射线上有两点在一个平面内, 则这条射线上所有的点都在这个平面内.A． ①②③ B． ②③④ C． ③④ D． ②③ 7．空间三条直线交于同一点，它们确定平面的个数为n，则n的可能取值为（ ） A． 1 B．1或3 C．1或2或3 D．1或 4 8．如果  那么下列关系成立的是（ ）A．  B． C． D． 9．空间中交于一点的四条直线最多可确定平面的个数为（ ） A．7个 B．6个 C． 5个 D．4个 10．两个平面重合的条件是它们的公共部分有（ ） A．两个公共点 B．三个公共点 C．四个公共点 D．两条平行直线 11．一条直线和直线外的三点所能确定的平面的个数是（ ） A． 1或3个 B．1或4个 C．1个、3个或4个 D． 1个、2个或4个 12．三条直线两两相交，可以确定平面的个数是（ ） A．1个 B．1个或2个 C．1个或3个 D．3个 13．空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点，如果EF  GH=P，则点P（ ）A．一定在直线BD上 B．一定在直线AC上 C．在直线AC或BD上 D．不在直线AC上也不在直线BD上 14．设平面 与平面 交于直线 , 直线 , 直线 , , 则M_______．15．直线AB、AD ，直线CB、CD ，点E AB，点FBC，点GCD，点HDA，若直线HE直线FG=M，则点M必在直线___________上．16．如图,在棱长为a的正方体ABCD-A1B1C1D1中，M、N分别 为AA1、C1D1的中点，过D、M、N三点的平面与直线A1B1交于 点P，则线段PB1的长为_______________．  17．如图, 正方体ABCD-A1B1C1D1中，对角线BD1与过A1、D、 C1的平面交于点M，则BM：MD1=________________．  18．如图，E、F、G、H分别是空间四边形AB、BC、CD、DA上的点，且EH与FG交于点O． 求证：B、D、O三点共线．  19．证明梯形是平面图形． 20．已知: 直线  , 且直线与a, b, c都相交． 求证: 直线 共面．21．在正方体ABCD-A1B1C1D1中, 直线A1C交平面ABC1D1于点M , 试作出点M的位置． 参考答案： 经典例题： 证明：连接EF，QG，  E，F，Q，G分别是A1D1，D1C1，A1A，C1C的中点， EF||A1C1||QG, 同理FG||EP，设E，F，G，Q确定平面，F，G，E，P确定平面 ，由于 都经过不共线的三点E，F，G，故重合，即E，F，G，P，Q五点共面，同理可证E，F，G，H，Q五点共面，故E，F，G，H，P，Q共面．当堂练习： 1.A; 2.B; 3.C; 4.B; 5.B; 6.B; 7.B; 8.A; 9.B; 10.D; 11.C; 12.C; 13.A; 14. ; 15. BD; 16.  ; 17. 2:1;18.证明：  E ，  .  . . 同理可证O ,  , 即B、D、O三点共线． 20.证明: 如图 ,设 与 分别交于A ,B ,C , 经过 可确定一个平面 经过a, b可确定一个平面. ,同理B ,则AB, 即 因经过  的平面有且只有一个,  与为同一平面. 同理 即共面． 21.解: 连结D1B , A1B , CD1, 则D1B与A1C的交点即为所求作的点M. 证明: 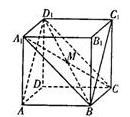D1B平面ABC1D1 , D1B平面A1BCD1 ,  平面ABC1D1平面A1BCD1= D1B.A1C平面ABC1D1=M, M平面AB C1D1, M平面A1BCD1 , MD1B．故M为D1B与A1C的交点． (责任编辑：admin) |