|
立体几何初步单元测试 1．  ∥ ，a，b与，都垂直，则a，b的关系是A．平行 B．相交 C．异面 D．平行、相交、异面都有可能 2．异面直线a，b，a⊥b，c与a成300，则c与b成角范围是 A．[600，900] B．[300，900] C．[600，1200] D．[300，1200] 3．正方体AC1中，E、F分别是AB、BB1的中点，则A1E与C1F所成的角的余弦值是 A．  B． C． D． 4．在正△ABC中，AD⊥BC于D，沿AD折成二面角B—AD—C后，BC=  AB，这时二面角B—AD—C大小为A．600 B．900 C．450 D．1200 5．一个山坡面与水平面成600的二面角，坡脚的水平线（即二面角的棱）为AB，甲沿山坡自P朝垂直于AB的方向走30m，同时乙沿水平面自Q朝垂直于AB的方向走30m，P、Q都是AB上的点，若PQ=10m，这时甲、乙2个人之间的距离为 A．  B． C． D． 6．E、F分别是正方形ABCD的边AB和CD的中点，EF交BD于O，以EF为棱将正方形 折成直二面角如图，则∠BOD= A．1350 B．1200 C．1500 D．900 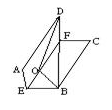 7．三棱锥V—ABC中，VA=BC，VB=AC，VC=AB，侧面与底面ABC所成的二面角分别为α，β，γ（都是锐角），则cosα+cosβ+cosγ等于 A．1 B．2 C． D． 8．正n棱锥侧棱与底面所成的角为α，侧面与底面所成的角为β，tanα∶tanβ等于 A．  B． C． D． 9．一个简单多面体的各面都是三角形，且有6个顶点，则这个简单多面体的面数是 A．4 B．6 C．8 D．10 10．三棱锥P—ABC中，3条侧棱两两垂直，PA=a，PB=b，PC=c，△ABC的面积为S，则P到平面ABC的距离为 A．  B． C． D． 11．三棱柱ABC—A1B1C1的体积为V，P、Q分别为AA1、CC1上的点，且满足AP=C1Q，则四棱锥B—APQC的体积是 A．  B． C． D． 12．多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，EF=  ，EF与面AC的距离为2，则该多面体的体积为A．  B．5 C．6 D． 13．已知异面直线a与b所成的角是500，空间有一定点P，则过点P与a，b所成的角都是300的直线有________条． 14．线段AB的端点到平面α的距离分别为6cm和2cm，AB在α上的射影A’B’的长为3cm，则线段AB的长为__________． 15．正n棱锥相邻两个侧面所成二面角的取值范围是____________． 16．如果一个简单多面体的每个面都是奇数的多边形，那么它的面数是__________． 17．在正方体ABCD—A1B1C1D1中，E、F、G、H分别为棱BC、CC1、C1D1、AA1的中点，O为AC与BD的交点． 求证：（1）EG∥平面BB1D1D；（2）平面BDF∥平面B1D1H；（3）A1O⊥平面BDF；（4）平面BDF⊥平面AA1C． 18．如图，三棱锥D—ABC中，平面ABD、平面ABC均为等腰直角三角形， ∠ABC=∠BAD=900，其腰BC=a，且二面角D—AB—C=600． ⑴求异面直线DA与BC所成的角；⑵求异面直线BD与AC所成的角； ⑶求D到BC的距离； ⑷求异面直线BD与AC的距离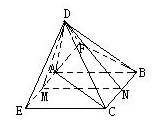．  19．如图，在600的二面角α—CD—β中，AC 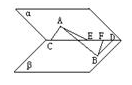 α，BDβ，且ACD=450，tg∠BDC=2，CD=a，AC= x，BD= x，当x为何值时，A、B的距离最小？并求此距离． 20．如图，斜三棱柱ABC—A’B’C’中，底面是边长为a的正三角形，侧棱长为 b，侧棱AA’与底面相邻两边AB、AC都成450角，求此三棱柱的侧面积和体积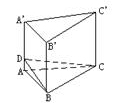．  参考答案： 1.D; 2.A; 3.C; 4.A; 5.B; 6.B; 7.A; 8.B; 9.C; 10.B; 11.B; 12.D; 13.2; 14. 5或  ; 15. （ ）; 16. 偶数; 17. 解析：  ⑴欲证EG∥平面BB1D1D，须在平面BB1D1D内找一条与EG平行的直线，构造辅助平面BEGO’及辅助直线BO’，显然BO’即是。⑵按线线平行  线面平行面面平行的思路，在平面B1D1H内寻找B1D1和O’H两条关键的相交直线，转化为证明：B1D1∥平面BDF，O’H∥平面BDF⑶A1O⊥平面BDF，由三垂线定理，易得BD⊥A1O，再寻A1O垂直于平面BDF内的另一条直线。猜想A1O⊥OF。借助于正方体棱长及有关线段的关系计算得：A1O2+OF2=A1F2 A1O⊥OF。⑷∵ CC1⊥平面AC∴ CC1⊥BD 又BD⊥AC∴ BD⊥平面AA1C 又BD 平面BDF∴ 平面BDF⊥平面AA1C 18. 解析： 在平面ABC内作AE∥BC，从而得∠DAE=600 ∴ DA与BC成600角 过B作BF∥AC，交EA延长线于F，则∠DBF为BD与AC所成的角 由△DAF易得AF=a，DA=a，∠DAF=1200∴ DF2=a2+a2-2a2·(  )=3a2 ∴ DF= aDBF中，BF=AC= a∴ cos∠DBF= ∴ 异面直线BD与AC成角arccos（3）∵ BA⊥平面ADE∴ 平面DAE⊥平面ABC 故取AE中点M，则有DM⊥平面ABC；取BC中点N，由MN⊥BC，根据三垂线定理，DN⊥BC  ∴ DN是D到BC的距离 在△DMN中，DM= a，MN=a∴ DN= a（4）∵ BF 平面BDF，AC 平面BDF，AC∥BF∴ AC∥平面BDF 又BD平面BDF∴ AC与BD的距离即AC到平面BDF的距离∵  ， ∴   由  ，即异面直线BD与AC的距离为 .19. 解析：作AE⊥CD于E，BF⊥CD于F，则EF为异面直线AE、BF的公垂段，AE与BF成600角，可求得|AB|=  ，当x= 时，|AB|有最小值 .20. 解析：在侧面AB’内作BD⊥AA’于D 连结CD ∵ AC=AB，AD=AD，∠DAB=∠DAC=450 ∴ △DAB≌△DAC ∴ ∠CDA=∠BDA=900，BD=CD ∴ BD⊥AA’，CD⊥AA’∴ △DBC是斜三棱柱的直截面 在Rt△ADB中，BD=AB·sin450=   ∴ △DBC的周长=BD+CD+BC=( +1)a，△DBC的面积= ∴ S侧=b(BD+DC+BC)=( +1)ab ∴ V= ·AA’= (责任编辑：admin) |