|
南昌市高中新课程训练题（直线、平面、简单几何体1） 命题：莲塘一中 李鸿斌 一、选择题（本小题共12小题，每小题5分，共60分） 1. 若  是平面 外一点，则下列命题正确的是（A）过 只能作一条直线与平面相交 （B）过可作无数条直线与平面垂直（C）过 只能作一条直线与平面平行 （D）过可作无数条直线与平面平行2．在空间四边形  中， 、 、 、 上分别取 、 、 、 四点，如果 、 交于一点 ，则（ ）A． 一定在直线 上 B．一定在直线 上C． 在直线或上 D．既不在直线上，也不在上3．如图S为正三角形所在平面ABC外一点，且SA＝SB＝SC＝AB，E、F分别为SC、AB中点，则异面直线EF与SA所成角为（ ） A．90? B．60? C．45? D．30? 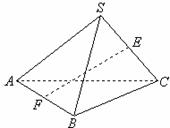 4．下列说法正确的是（ ） A．若直线  平行于平面 内的无数条直线，则 B．若直线  在平面外，则 C．若直线  ， ，则D．若直线 ，，则直线就平行于平面内的无数条直线5．在下列条件中，可判断平面 与平面 平行的是（ ）A． 、都垂直于平面 B． 内存在不共线的三点到平面的距离相等C． 、 是内两条直线，且 ， D． 、是两条异面直线，且， ，，6 若  为一条直线， 为三个互不重合的平面，给出下面三个命题：①  ②  ；③  ，其中正确的命题有（ ）A. 0个 B. 1个 C. 2个 D. 3个 7．把正方形ABCD沿对角线AC折起，当点D到平面ABC的距离最大时，直线BD和平面ABC所成角的大小为 （ ） A．90? B．60? C．45? D．30? 8．PA、PB、PC是从点P引出的三条射线，每两条射线的夹角均为60?，则直线PC与平面APB所成角的余弦值是（ ） A．  B． C． D． 9．正方体ABCD—A1B1C1D1中，E、F分别是AA1、AB的中点，则EF与对角面A1C1CA所成角的度数是（ ） A．30? B．45? C．60? D．150? 10．设A、B、C、D是空间四个不同的点，在下列命题中，不正确的是 （A）若AC与BD共面，则AD与BC共面 （B）若AC与BD是异面直线，则AD与BC是异面直线 （C）若AB=AC，DB=DC，则AD=BC （D）若AB=AC，DB=DC，则AD⊥BC 11．对于平面 和共面的直线 、 下列命题中真命题是（A）若  则 （B）若 则 （C）若  则 （D）若、 与所成的角相等，则12．给出以下四个命题： ①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行， ②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面 ③如果两条直线都平行于一个平面，那么这两条直线互相平行， ④如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直. 其中真命题的个数是 A.4 B. 3 C. 2 D. 1 二、填空题（本大题共4小题，每小题4分，共16分） 13．设  是直二面角， ， ， ， ，则  。14． 、、是两两垂直且交于O点的三个平面，P到平面、、的距离分别是2、3、6，则  。15． 如图，在正三棱柱  中，AB=1。若二面角 的大小为 ，则点 到直线AB的距离为 。 16．已知正四棱锥的体积为12，底面对角线的长为  ，则侧面与底面所成的二面角等于_______________三、解答题（本大题共6小题，共74分） 17.如图，ABCD-A1B1C1D1是正四棱柱。 （I）求证：BD⊥平面ACC1A； （II）若二面角C1-BD-C的大小为60°，求异面直线BC1与AC所成角的大小。  18．如图，在直三棱柱ABC—A1B1C1中，AA1＝2，  ， ，⑴求证：平面AB1C⊥平面BB1C； ⑵求点B到平面AB1C的距离。  19. 如图1，已知ABCD是上．下底边长分别为2和6，高为  的等腰梯形，将它沿对称轴OO1折成直二面角，如图2.（Ⅰ）证明：AC⊥BO1； （Ⅱ）求二面角O－AC－O1的大小. 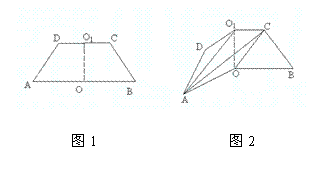  20．如图，△ABC和△DBC所在平面互相垂直，且AB＝BC＝BD，∠ABC＝∠DBC＝120?， 求：⑴A、D连线和平面DBC所成的角；⑵二面角A—BD—C的正切值。 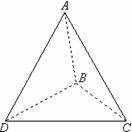 21． 如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，面CDE是等边三角形，棱  。（1）证明FO//平面CDE； （2）设 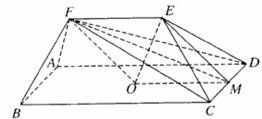 ，证明EO⊥平面CDF。 22.（本小题满分12分） 如图，四面体ABCD中，O、E分别是BD、BC的中点，  （I）求证：  平面BCD；（II）求异面直线AB与CD所成角的大小； （III）求点E到平面ACD的距离。 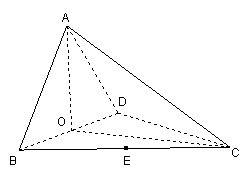 参考答案 一、选择题 DBCDD CCCAC CB 12．提示：BD1⊥平面AB1C，EF⊥平面AB1C 二、填空题 13．60? 14．7 15． 16．. 。三、解答题 17． 解法一： （1）∵ABCD-A1B1C1D1是正四棱柱 ∴CC1⊥平面ABCD ∴BD⊥CC1 ∴ABCD是正方形， ∴BD⊥AC 又∵AC，CC1  平面ACC1A1，且AC∩CC1=C，∴BD⊥平面ACC1A1 （II）设BD与AC相交于O，连接C1O。 ∵CC1⊥平面ABCD、BD⊥AC。∴BD⊥C1O∴∠C1OC是二面角C1-BD-C的平面角 ∴∠C1OC=60° 连接A1B∵A1C1∥AC∴∠A1C1B是BC1与AC所成角. 设BC=a,则CO=   在△A1BC1中，由余弦定理得 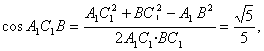  ∴异面直线BC1与AC所成角的大小为arccos  解法二:（I）建立空间直角坐标系D-xyz,如图。  设AD=a，DD1=b，则有D（0，0，0），A（a，0，0），B（a，a，0）， C（0，a，0），C1（0，a，b），  ∴BD⊥AC，BD⊥CC1 又∵AC，CC1  平面ACC1A1，且AC∩CC1=C，∴BD⊥平面ACC1A1。 （II）设BD与AC相交于O，连接C1O，则点O坐标为  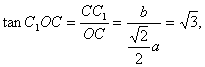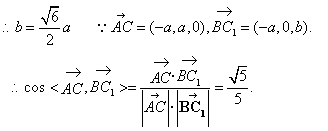) ∴BD⊥C1O，又BD⊥CO， ∴∠C1OC=60°∴   ∴异面直线BC1与AC所成角的大小为  18．⑴由已知条件立即可证得，  ⑵在平面BB1C内作BD⊥B1C于D，由⑴得BD⊥面AB1C， ∴BD为B到面AB1C的距离，∴  （本题也可用体积转换）19．．解法一（I）证明 由题设知OA⊥OO1，OB⊥OO1. 所以∠AOB是所折成的直二面角的平面角， 即OA⊥OB. 故可以O为原点，OA、OB、OO1 所在直线分别为  轴、y轴、z轴建立空间直角坐标系，如图3，则相关各点的坐标是A（3，0，0），B（0，3，0），C（0，1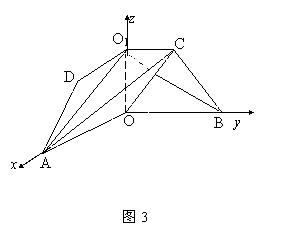， ）O1（0，0，）.  从而  所以AC⊥BO1. （II）解：因为  所以BO1⊥OC，由（I）AC⊥BO1，所以BO1⊥平面OAC，  是平面OAC的一个法向量.设  是0平面O1AC的一个法向量，由  得 . 设二面角O—AC—O1的大小为  ，由 、的方向可知 ，>，所以cos  ，>= 即二面角O—AC—O1的大小是  解法二（I）证明 由题设知OA⊥OO1，OB⊥OO1，所以∠AOB是所折成的直二面角的平面角，即OA⊥OB. 从而AO⊥平面OBCO1，OC是AC在面OBCO1内的射影. 因为   ，所以∠OO1B=60°，∠O1OC=30°，从而OC⊥BO1 由三垂线定理得AC⊥BO1.   （II）解 由（I）AC⊥BO1，OC⊥BO1，知BO1⊥平面AOC. 设OC∩O1B=E，过点E作EF⊥AC于F，连结O1F（如图4），则EF是O1F在平面AOC 内的射影，由三垂线定理得O1F⊥AC. 所以∠O1FE是二面角O—AC—O1的平面角. 由题设知OA=3，OO1= ，O1C=1，所以  ，从而  ， 又O1E=OO1·sin30°= ，⑴显然可得MN∥平面ABC，∵平面MNC  平面ABC＝，∴MN∥⑵∵PC⊥平面ABC，∴平面PAC⊥平面ABC，作MQ⊥AC，则MQ⊥平面ABC， 作QD⊥ 于D，则MD⊥，MD的长即为M到的距离在Rt△ACB中，可求得  ，又 ，∠QCD＝30?，∴  ， ，于是 20．⑴作AO⊥BC交BC的延长线于O，∵面ABC⊥面BCD，∴OA⊥面BCD，连OD，则∠ADO就是AD与平面BCD所成的角，可求得∠ADO＝45? ⑵作OE⊥BD于E，连AE，则BD⊥AE， ∴∠AEO就是二面角A－BD－C的平面角的补角， ∵∠ABO＝60?，∴  ， ，∵∠EBO＝60?，∴ 在Rt△AOE中，  ，∴二面角A－BD－C的正切值为－221. （1）证明：取CD中点M，连结OM，在矩形ABCD中  ，又，则 。连结EM，于是四边形EFOM为平行四边形 ∴ FO//EM 又 ∵ FO  平面CDE，且EM平面CDE，∴ FO//平面CDE（2）证明：连结FM，由（1）和已知条件，在等边  中，CM=DM，EM⊥CD且 。因此平行四边形EFOM为菱形，从而EO⊥FM∵ CD⊥OM，CD⊥EM ∴ CD⊥平面EOM，从而CD⊥EO 而FM  CD=M，所以 平面CDF22（I）证明：连结OC   在  中，由已知可得 而    即   平面  （II）解：取AC的中点M，连结OM、ME、OE，由E为BC的中点知   直线OE与EM所成的锐角就是异面直线AB与CD所成的角在  中，  是直角斜边AC上的中线，  异面直线AB与CD所成角的大小为 （III）解：设点E到平面ACD的距离为   在  中，  而   点E到平面ACD的距离为 (责任编辑：admin) |