|
2.1.1 函数的概念和图象 重难点：在对应的基础上理解函数的概念并能理解符号“y=f（x）”的含义，掌握函数定义域与值域的求法； 函数的三种不同表示的相互间转化，函数的解析式的表示，理解和表示分段函数；函数的作图及如何选点作图，映射的概念的理解． 考纲要求：①了解构成函数的要素，会求一些简单函数的定义域和值域； ②在实际情境中，会根据不同的需要选择恰当的方法（如图象法、列表法、解析法）表示函数； ③了解简单的分段函数，并能简单应用； 经典例题：设函数f（x）的定义域为［0，1］，求下列函数的定义域： （1）H（x）=f（x2+1）； （2）G（x）=f（x+m）+f（x－m）（m＞0）. 当堂练习： 1． 下列四组函数中,表示同一函数的是（ ） A．  B． C．  D． 2  函数 的图象与直线 交点的个数为（ ）A．必有一个 B．1个或2个 C．至多一个 D．可能2个以上 3．已知函数 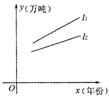 ，则函数 的定义域是（ ）A．  B． C． D． 4．函数  的值域是（ ）A．  B． C．  D．  5．对某种产品市场产销量情况如图所示，其中： 表示产品各年年产量的变化规律； 表示产品各年的销售情况．下列叙述： （ ）（1）产品产量、销售量均以直线上升，仍可按原生产计划进行下去； （2）产品已经出现了供大于求的情况，价格将趋跌； （3）产品的库存积压将越来越严重，应压缩产量或扩大销售量； （4）产品的产、销情况均以一定的年增长率递增．你认为较合理的是( ) A．（1），（2），（3） B．（1），（3），（4） C．（2），（4） D．（2），（3） 6．在对应法则  中,若 ,则 ，  6． 7．函数  对任何 恒有 ，已知 ，则 ．8．规定记号“  ”表示一种运算，即 . 若 ，则函数 的值域是___________．9．已知二次函数f(x)同时满足条件： (1) 对称轴是x=1； (2) f(x)的最大值为15；(3) f(x)的两根立方和等于17．则f(x)的解析式是 ． 10．函数  的值域是 ．11． 求下列函数的定义域 ： (1)  (2) 12．求函数  的值域．13．已知f(x)=x2+4x+3，求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t)． 14．在边长为2的正方形ABCD的边上有动点M，从点B开始，沿折线BCDA向A点运动，设M点运动的距离为x，△ABM的面积为S． （1）求函数S=的解析式、定义域和值域； （2）求f[f(3)]的值． 参考答案： 经典例题： 解：（1）∵f（x）的定义域为［0，1］， ∴f（x2+1）的定义域满足0≤x2+1≤1． ∴－1≤x2≤0． ∴x=0． ∴函数的定义域为｛0｝． （2）由题意，得  得 则①当1－m＜m，即m＞  时，无解； ②当1－m=m，即m=时，x=m=；③当1－m＞m＞0，即0＜m＜ 时，m≤x≤1－m．综上所述，当0＜m≤ 时，G（x）的定义域为{x|m≤x≤1－m}．当堂练习： 1. A ; 2. C ; 3. C ;4. D ;5. D ; 6. 5,  ;7.  ;8.  ;9. f(x)= -6x2+12x+9; 10. ;11.(1)  ,(2)由 得(- ,-1) (-1,0)．12. 设 ，则 ，当 时，y有最小值 ,所求函数的值域为 .13. 解：因抛物线的对称轴是x= -2,所以分类讨论: (1) ①当t+1<-2,即t<-3时, g(t)=f(t+1);②当  ,即 时g(t)=f(-2);③当t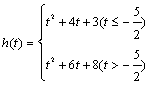>-2时, g(t)=f(t)．(2) ①当 -2-t  (t+1)-(-2), 即t 时, h(t)= f(t); ②当-2-t< (t+1)-(-2), 即t 时, h(t)= f(t+1)．综上所述:  , 14. 解：（1）当  时，S=x；当 时，S=2；当 时，S=6-x。 定义域是（0，6），值域是（0，2） (2) f[f(3)]=f(2)=2． (责任编辑：admin) |