|
2.1.2 函数的简单性质 重难点：领会函数单调性的实质，明确单调性是一个局部概念，并能利用函数单调性的定义证明具体函数的单调性，领会函数最值的实质，明确它是一个整体概念，学会利用函数的单调性求最值；函数奇偶性概念及函数奇偶性的判定；函数奇偶性与单调性的综合应用和抽象函数的奇偶性、单调性的理解和应用；了解映射概念的理解并能区别函数和映射． 考纲要求：①理解函数的单调性、最大（小）值及其几何意义；结合具体函数，了解函数奇偶性的含义；并了解映射的概念； ②会运用函数图像理解和研究函数的性质． 经典例题：定义在区间（－∞，＋∞）上的奇函数f（x）为增函数，偶函数g（x）在［0，＋∞ )上图象与f（x）的图象重合.设a＞b＞0，给出下列不等式，其中成立的是 f（b）－f（－a）＞g（a）－g（－b） ②f（b）－f（－a）＜g（a）－g（－b） ③f（a）－f（－b）＞g（b）－g（－a） ④f（a）－f（－b）＜g（b）－g（－a） A．①④ B．②③ C．①③ D．②④ 当堂练习： 1．已知函数f(x)=2x2-mx+3，当  时是增函数，当 时是减函数，则f(1)等于 （ ）A．-3 B．13 C．7 D．含有m的变量 2．函数 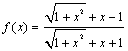 是（ ）A． 非奇非偶函数 B．既不是奇函数,又不是偶函数奇函数 C． 偶函数 D． 奇函数 3．已知函数(1)  , (2) ,(3) (4)  ,其中是偶函数的有（ ）个A．1 B．2 C．3 D．4 4．奇函数y=f（x）（x≠0），当x∈（0，+∞）时，f（x）=x－1，则函数f（x－1）的图象为 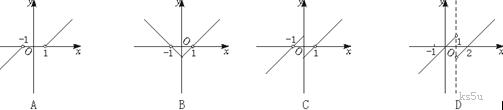（ ）  5．已知映射f:A  B,其中集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中元素在映射f下的象,且对任意的 ,在B中和它对应的元素是 ,则集合B中元素的个数是（ ）A．4 B．5 C．6 D．7 6．函数  在区间[0, 1]上的最大值g(t)是 ．7． 已知函数f(x)在区间  上是减函数,则 与 的大小关系是 ．8．已知f(x)是定义域为R的偶函数,当x<0时, f(x)是增函数,若x1<0,x2>0,且  ,则 和 的大小关系是 ．9．如果函数y=f(x+1)是偶函数，那么函数y=f(x)的图象关于_________对称． 10．点(x,y)在映射f作用下的对应点是  ,若点A在f作用下的对应点是B(2,0),则点A坐标是 ．13. 已知函数  ,其中 ，(1)试判断它的单调性；(2)试求它的最小值．14．已知函数  ，常数 。（1）设  ，证明：函数 在 上单调递增；（2）设  且的定义域和值域都是 ，求 的最大值．13.(1)设f(x)的定义域为R的函数,求证:  是偶函数； 是奇函数.(2)利用上述结论，你能把函数  表示成一个偶函数与一个奇函数之和的形式．14. 在集合R上的映射:  , .(1)试求映射  的解析式;(2)分别求函数f1(x)和f2(z)的单调区间; (3) 求函数f(x)的单调区间. 参考答案： 经典例题： 解析：本题可采用三种解法. 方法一：直接根据奇、偶函数的定义． 由f（x）是奇函数得f（－a）=－f（a），f（－b）=－f（b），g（a）=f（a），g（b）=f（b），g（－a）=g（a），g（－b）=g（b）． ∴以上四个不等式分别可简化为①f（b）＞0；②f（b）＜0；③f（a）＞0；④f（a）＜0. 又∵f（x）是奇函数又是增函数，且a＞b＞0，故f（a）＞f（b）＞f（0）=0，从而以上不等式中①、③成立.故选C. 方法二：结合函数图象． 由下图，分析得f（a）=g（a）=g（－a）=－f（－a），f（b）=g（b）=g（－b）=－f（－b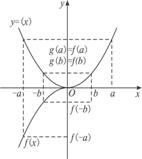）．  从而根据所给结论，得到①与③是正确的.故选C． 方法三：利用间接法，即构造满足题意的两个函数模型f（x）=x，g（x）=|x|，取特殊值a、b.如a=2，b=1.可验证正确的是①与③，故选C． 答案：C 当堂练习： B ; 2. D ; 3. B ;4. D ;5. A ; 6.  ;7.  ;8. >;9. x=-1; 10. ( );11. 解: (1)函数  ，设 时，   ，所以 在区间 上单调递增；(2)从而当x=1时，  有最小值 ．12. 解:（1）任取  ， ，且 ， ， 因为 ，，，所以 ，即 ，故 在 上单调递增．（2）因为 在上单调递增， 的定义域、值域都是  ，即  是方程 的两个不等的正根 有两个不等的正根．所以  ，  ∴  ，∴  时， 取最大值 ．13.解: (1)利用定义易证之； (2)由(1)得  = ． 14. 解: (1)  ； (2)当 时， f1(x)单调递减， 当 时， f1(x)单调递增； 当 时， f2(z) 单调递减， 当 时， f1(x)单调递增．(3) 当  和 时， f(x)分别单调递减；当  和 分别单调递增．(责任编辑：admin) |